题目内容
10.一根1米长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,第四次后剩下的绳子的长度是$\frac{1}{16}$ 米.第n次呢$\frac{1}{{2}^{n}}$.分析 第一次剪去一半后是($\frac{1}{2}$)1,第二次剪去剩下的一半后是($\frac{1}{2}$)2,第三次剪去剩下的一半后是($\frac{1}{2}$)3,依此类推,第四次剪去剩下的一半后是($\frac{1}{2}$)4,第n次剪去剩下的一半后是($\frac{1}{2}$)n
解答 解:1米长的绳子,第一次剪去一半后剩下$\frac{1}{2}$;
第二次剪去剩下的一半后剩下$\frac{1}{2}$的一半是$\frac{1}{4}$;
第三次再剪去$\frac{1}{4}$的一半后剩下$\frac{1}{8}$;
第三次再剪去$\frac{1}{8}$的一半剩下$\frac{1}{16}$.
第n次后剩下($\frac{1}{2}$)n=$\frac{1}{{2}^{n}}$.
故答案为:$\frac{1}{16}$,$\frac{1}{{2}^{n}}$.
点评 本题考查了有理数的乘方运算及规律探究.找到规律是解决本题的关键.

练习册系列答案
相关题目
18.计算:(-2)-1+(-1)0=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
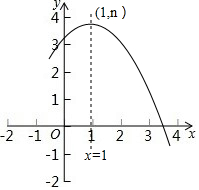 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论: 如图,已知AD所在直线是△ABC的对称轴,点E、F是AD上的两点,若BC=4,AD=3,则图中阴影部分的面积的值是3.
如图,已知AD所在直线是△ABC的对称轴,点E、F是AD上的两点,若BC=4,AD=3,则图中阴影部分的面积的值是3.