题目内容
15．
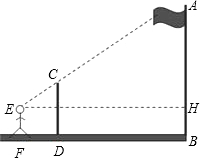九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，如图所示，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，则旗杆AB的高度13.5m．
分析 利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB=EF=1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出$\frac{CG}{AH}$=$\frac{EG}{EH}$，把相关条件代入即可求得AH=11.9m，得出AB的长即可．
解答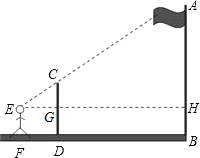 
解：∵CD⊥FB，AB⊥FB，
∴CD∥AB
∴△CGE∽△AHE
∴$\frac{CG}{AH}$=$\frac{EG}{EH}$
即：$\frac{CD-EF}{AH}$=$\frac{FD}{FD+BD}$，
∴$\frac{3-1.6}{AH}$=$\frac{2}{2+15}$，
解得：AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5（m）．
故答案为：13.5．
点评 此题主要考查了相似三角形的应用，解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
3．
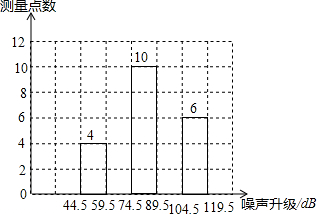为了增强人们的环境保护意识，某校若干名学生组成了“控制噪声污染”课题学习研究小组．在环保局工作人员帮助指导下，该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将调查的数据进行处理（设所测数据是正整数），得频数分布表如下：
根据表中提供的信息解答下列问题：
（1）表中的c值为0.3；
（2）补全频数分布直方图；
（3）如果全市共有200个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？
为了增强人们的环境保护意识，某校若干名学生组成了“控制噪声污染”课题学习研究小组．在环保局工作人员帮助指导下，该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将调查的数据进行处理（设所测数据是正整数），得频数分布表如下：| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5--59.5 | 4 | 0.1 |
| 2 | 59.5--74.5 | a | 0.2 |
| 3 | 74.5--89.5 | 10 | 0.25 |
| 4 | 89.5--104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
（1）表中的c值为0.3；
（2）补全频数分布直方图；
（3）如果全市共有200个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？
