题目内容
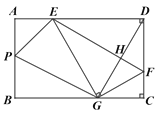
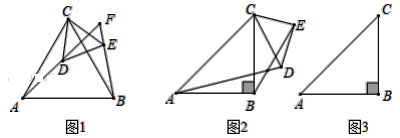
【题目】(1)如图1，△ABC和△CDE均为等边三角形，直线AD和直线BE交于点F．
①求证：AD＝BE；
②求∠AFB的度数．
(2)如图2，△ABC和△CDE均为等腰直角三角形，∠ABC＝∠DEC＝90°，直线AD和直线BE交于点F．
①求证：AD＝
BE；
②若AB＝BC＝3，DE＝EC＝．将△CDE绕着点C在平面内旋转，当点D落在线段BC上时，在图3中画出图形，并求BF的长度．
【答案】（1）①见详解，②60°；（2）①见详解，②
．
【解析】
（1）如图①先判断出
，即可得出结论；
②求出
，即可得出结论；
（2）①先判断出
，得出
，即可得出结论；
②如图，先求出
，进而判断出，得出
，进而判断出
，即可得出结论．
解：（1）①
和
均为等边三角形，
，
，
．
．
．
，
．
②如图1，设
交
于点
．
，，
．
即
．
（2）①∵△ABC和△CDE均为等腰直角三角形，
，
，
，
，
．
．
．
．
．
②当点
落在线段上时，
如图，则
，
．
过点
作
于点
，
则
，
．
，．
．
．
又
，
．
．
又
，
．
．
．
．
练习册系列答案
相关题目
