题目内容
【题目】二次函数y=ax2+2x﹣2,若对满足3<x<4的任意实数x都有y>0成立,则实数a的取值范围为_____.
【答案】a>-![]()
【解析】
方法1:由题意可得ax2+2x-2>0,即为a>![]() 对3<x<4成立,求得右边函数的取值范围,即可得到所求a的范围.
对3<x<4成立,求得右边函数的取值范围,即可得到所求a的范围.
方法二:分情况讨论:①![]() 时,抛物线开口向上,
时,抛物线开口向上,![]() 时符合题意,
时符合题意,![]() 时,由于抛物线对称轴在y轴左侧,可知x=3时y>0,则符合题意;②
时,由于抛物线对称轴在y轴左侧,可知x=3时y>0,则符合题意;②![]() 时,抛物线开口向下,则同时满足x=3,x=4时,y>0,则符合题意.
时,抛物线开口向下,则同时满足x=3,x=4时,y>0,则符合题意.
方法一:解:若对满足3<x<4的任意实数x都有y>0成立,
即有ax2+2x﹣2>0,即为a>![]() ,且 3<x<4,
,且 3<x<4,
由y=![]() 在3<x<4内y随x的增大而增大,
在3<x<4内y随x的增大而增大,
因为当x=3,可得y=![]() =﹣
=﹣![]() ,当x=4,可得y=
,当x=4,可得y=![]() =﹣
=﹣![]() ,
,
所以﹣![]() <
<![]() <﹣
<﹣![]() ,
,
所以a>-![]()
有∵a≠0,
故答案为:a>-![]() 且a≠0.
且a≠0.
方法二:解:①当![]() 时,抛物线开口向上,
时,抛物线开口向上,
若![]() ,则对于任意实数x都有y>0,
,则对于任意实数x都有y>0,
即![]() ,解得
,解得![]() ,
,
与![]() 矛盾,此种情况不存在;
矛盾,此种情况不存在;
若![]() ,即
,即![]() ,解得
,解得![]()
∵抛物线对称轴![]()
∴抛物线在3<x<4时y随x的增大而增大
当x=3时,y>0,则满足3<x<4的任意实数x都有y>0成立
即9a+6-2>0,解得![]()
∴![]() 时,满足3<x<4的任意实数x都有y>0成立
时,满足3<x<4的任意实数x都有y>0成立
②当![]() 时,抛物线开口向下
时,抛物线开口向下
同时满足x=3,x=4时,y>0,则满足3<x<4的任意实数x都有y>0成立
即![]()
解得![]()
∴![]()
故答案为:![]() 或
或![]()

 名校课堂系列答案
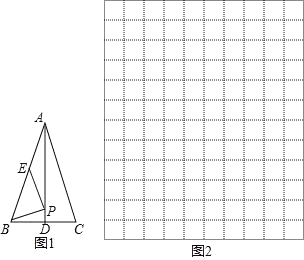
名校课堂系列答案【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.