题目内容
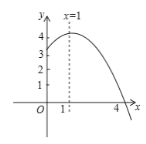
【题目】如图，将函数y=
（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】试题解析：∵函数y=
（x-2）2+1的图象过点A（1，m），B（4，n），
∴m=
（1-2）2+1=1
，n=
（4-2）2+1=3，
∴A（1， 
），B（4，3），
过A作AC∥x轴，交B′B的延长线于点C，则C（4， 
），
∴AC=4-1=3，
∵曲线段AB扫过的面积为9（图中的阴影部分），
∴ACAA′=3AA′=9，
∴AA′=3，
即将函数y=
（x-2）2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象，
∴新图象的函数表达式是y=
（x-2）2+4．
故选D．
练习册系列答案
习题精选系列答案
相关题目
