题目内容
有面额为壹元、贰元、伍元的人民币共10张，欲用来购买一盏价值为18元的护眼灯，要求三种面额都用上，则不同的付款方式有（ ）
| A、8种 | B、7种 | C、4种 | D、3种 |
考点：三元一次不定方程
专题：
分析：设一元x张，二元y张，五元z张，欲用来购买一盏价值为18元的护眼灯，要求三种面额都用上，只要所选面额之和为18元，总张数小于等于10即可，进而分析得出答案．
解答：解：设一元x张，二元y张，五元z张，
由题意得，x+y+z=10，
∵欲用来购买一盏价值为18元的护眼灯，要求三种面额都用上，
∴只要所选面额之和为18元，总张数小于等于10即可，
当5元的1张，2元的为：4张，1元的为：5张，
当5元的1张，2元的为：5张，1元的为：3张，
当5元的1张，2元的为：6张，1元的为：1张，
当5元的2张，2元的为：3张，1元的为：2张，
当5元的2张，2元的为：2张，1元的为：4张，
当5元的2张，2元的为：1张，1元的为：6张，
当5元的3张，2元的为：1张，1元的为：2张，
则符合要求的付款方式共7种，
故选B．
由题意得，x+y+z=10，
∵欲用来购买一盏价值为18元的护眼灯，要求三种面额都用上，
∴只要所选面额之和为18元，总张数小于等于10即可，
当5元的1张，2元的为：4张，1元的为：5张，
当5元的1张，2元的为：5张，1元的为：3张，
当5元的1张，2元的为：6张，1元的为：1张，
当5元的2张，2元的为：3张，1元的为：2张，
当5元的2张，2元的为：2张，1元的为：4张，
当5元的2张，2元的为：1张，1元的为：6张，
当5元的3张，2元的为：1张，1元的为：2张，
则符合要求的付款方式共7种，
故选B．
点评：此题主要考查了三元一次不定方程的应用，根据已知得出欲用来购买一盏价值为18元的护眼灯，要求三种面额都用上，只要所选面额之和为18元，总张数小于等于10即可，进而得出是解题关键．
练习册系列答案
智慧小复习系列答案
相关题目
如图，在四边形纸片ABCD中，∠A=100°，∠C=40°，现将其右下角向内翻折得△FGE，折痕为EF，恰使GF∥CD，GE∥AD，则∠B=若A（a，-b），B（-b，a）表示同一个点，那这个点一定在（ ）
| A、第二、四象限的角平分线上 |
| B、第一、三象限的角平分线上 |
| C、平行于x轴的直线上 |
| D、平行于y轴的直线上 |
由若干块形状相同的小正方块搭成的立体模型的主视图与俯视图如下，则不同的搭法总数为（ ）| A、1 | B、2 | C、3 | D、4 |
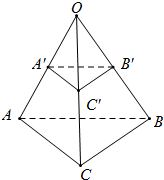如图所示，不共面的三条直线交于O点，在O点的同侧上分别取点A和A′，B和B′，C和C′，使得