题目内容
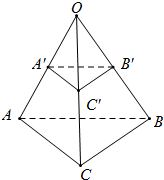如图所示，不共面的三条直线交于O点，在O点的同侧上分别取点A和A′，B和B′，C和C′，使得| OA |
| OA′ |
| OB |
| OB′ |
| OC |
| OC′ |
考点：相似三角形的判定
专题：证明题
分析：利“平行线截线段成比例”推知△ABC与△A′B′C′的对应边相互平行，则△ABC∽△A′B′C′．
解答：证明：如图，∵
=
，
∴A′B′∥AB，
∴
=
．
同理A′C′∥AC，B′C′∥BC，
∴
=
=
，
∴
=
=
．
∴△ABC∽△A′B′C′．
证明：如图，∵| OA |
| OA′ |
| OB |
| OB′ |
∴A′B′∥AB，
∴
| A′B′ |
| AB |
| OA |
| OA′ |
同理A′C′∥AC，B′C′∥BC，
∴
| A′C′ |
| AC |
| B′C′ |
| BC |
| OA |
| OA′ |
∴
| A′B′ |
| AB |
| A′C′ |
| AC |
| B′C′ |
| BC |
∴△ABC∽△A′B′C′．
点评：本题考查了相似三角形的判定．此题根据已知条件判定△ABC与△A′B′C′的对应边成比例来证得结论．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
有面额为壹元、贰元、伍元的人民币共10张，欲用来购买一盏价值为18元的护眼灯，要求三种面额都用上，则不同的付款方式有（ ）
| A、8种 | B、7种 | C、4种 | D、3种 |
甲：
=
=
-
乙：
=
=
-
对于他们的解，正确的判断是（ ）
| 2 | ||||
|
2(
| ||||||||
(
|
| 7 |
| 5 |
乙：
| 2 | ||||
|
(
| ||||||||
|
| 7 |
| 5 |
对于他们的解，正确的判断是（ ）
| A、甲乙都正确 |
| B、甲正确，乙不正确 |
| C、甲不正确，乙正确 |
| D、甲乙都不正确 |
下列各命题的逆命题成立的是（ ）
| A、如果两个角都是45°，那么这两个角相等 |
| B、全等三角形的对应角相等 |
| C、两直线平行，同位角相等 |
| D、如果两个数相等，那么它们的绝对值相等 |
如图，AD⊥BC于D，若AB+BD=DC，那么∠B与∠C有何数量关系？说明理由．