题目内容
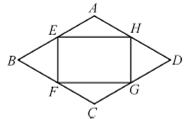
如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形的边长AB=4米,∠ABC=60°.设AE=x米(0<x<4),矩形的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草.已知红色花草的价格为20元/米2,黄色花草的价格为40元/米2.当x为何值时,购买花草所需的总费用最低,并求出最低总费用(结果保留根号).
(1)连接AC,BD.AC与EH的交点为M.
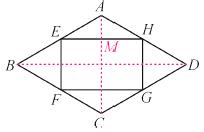
∵花坛为轴对称图形,
∴EH∥BD,EF∥AC.
∴△BEF∽△BAC.
∵∠ABC=60°,∴△ABC,△BEF是等边三角形.
∴EF=B E=AB-AE=4-x.
E=AB-AE=4-x.
在Rt△AEM中,∠AEM=∠ABD=30°,
则EM=AE·cos∠AEM=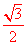 x.
x.
∴EH=2EM= x.
x.
∴S=EH·EF= x·(4-x).
x·(4-x).
即S=- x2+4
x2+4 x.
x.
(2)∵红色花草价格比黄色花草便宜,
∴当矩形面积最大时,购买花草的总费用最低.
又∵S=- x2+4
x2+4 x=-
x=- (x-2)2+4
(x-2)2+4 ,
,
∴当x=2时,S最大=4 .易得S四边形ABCD=8
.易得S四边形ABCD=8 .
.
此时四个三角形的面积为8 -4
-4 =4
=4 (米2).
(米2).
∴最低总费用为:20×4 +40×4
+40×4 =240
=240 (元).
(元).
答:当x=2时,购买花草所需的总费用最低,最低总费用是240 元.
元.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 (x<0)的图象经过顶点C,则k的值为 .
(x<0)的图象经过顶点C,则k的值为 .
 5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系y=-
5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系y=-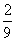 x2+
x2+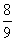 x+
x+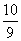 ,则羽毛球飞出的水平距离为 米.
,则羽毛球飞出的水平距离为 米.