题目内容
8. 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长为( )
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长为( )| A. | 8 | B. | 8.5 | C. | 9 | D. | 11 |
分析 先根据角平分线的定义及平行线的性质证明△BDO和△CEO是等腰三角形,再由等腰三角形的性质得BD=DO,CE=EO,则△ADE的周长=AB+AC,从而得出答案.
解答 解:∵BO平分∠ABC,
∴∠DBO=∠CBO,
∵DE∥BC,
∴∠CBO=∠DOB,
∴∠DBO=∠DOB,
∴BD=DO,
同理OE=EC,
∴△ADE的周长=AD+AE+ED=AB+AC=5+6=11.
故选D.
点评 本题考查等腰三角形的性质,平行线的性质及角平分线的性质.有效的进行线段的等量代换是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图的几何体的俯视图是( )
如图的几何体的俯视图是( )
 如图的几何体的俯视图是( )
如图的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
7.二次函数y=-(x-2)2-1的图象的顶点坐标是( )
| A. | (2,-1) | B. | (-2,-1) | C. | (-2,1) | D. | (2,1) |
20. 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )| A. | 132° | B. | 134° | C. | 136° | D. | 138° |
18.小亮在用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了下面的表格:
由于粗心,他算错了其中一个y值,则这个错误的y值是-2.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -2 | -3 | -4 | -3 | 0 | … |
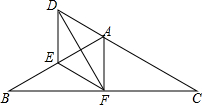 如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.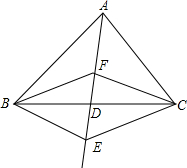 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE. 如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )
如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )


