题目内容
6.已知:梯形ABCD中,AD∥BC,AD:BC=2:5,F为AD的中点,E为BC上的点,且BE:EC=2:3,EF、CD的延长线交于G,则S△GFD:S△FED:S△DEC为1:2:6.分析 首先根据题意画出几何图形,再设AD=2,则BC=5,FD=1,EC=3,GF:GE=FD:EC=1:3,GF:FE=1:2,S△GFD:S△FED=GF:FE=1:2,S△EFD:S△CED=FD:EC=1:3即可得出答案.
解答 解:如图所示:
设AD=2,则BC=5,FD=1,EC=3,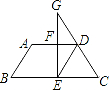
∵GF:GE=FD:EC=1:3,GF:FE=1:2,S△GFD:S△FED=GF:FE=1:2,
显然有S△EFD:S△CED=FD:EC=1:3,
∴S△GFD:S△FED:S△CED=1:2:6.
故答案为:1:2:6.
点评 本题考查了相似三角形的性质以及梯形的有关知识,属于基础题,正确运用边的比例关系求解是解题关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.若(a+b)2=12,(a-b)2=6,则ab的值是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 5 | D. | -5 |
8.把弯曲的河道改直,能够缩短航程,这样做的道理是( )
| A. | 两点之间,射线最短 | B. | 两点确定一条直线 | ||
| C. | 两点之间,直线最短 | D. | 两点之间,线段最短 |
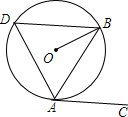 如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°.
如图,AB是⊙O的弦,AC与⊙O相切于点A,且∠BAC=52°. 如图,图形2可以看作图形1先向下平移2格,再向左平移1格得到.
如图,图形2可以看作图形1先向下平移2格,再向左平移1格得到.



 菱形ABCD的对角线AC、BD的长分别为4和2,若直线l满足:①点A到直线l的距离为$\sqrt{3}$;②B、D两点到直线l的距离相等.则符合题意的直线l的条数为( )
菱形ABCD的对角线AC、BD的长分别为4和2,若直线l满足:①点A到直线l的距离为$\sqrt{3}$;②B、D两点到直线l的距离相等.则符合题意的直线l的条数为( )