题目内容
 用两个直角边分别为a,b,斜边为c的全等直角三角形,按如图所示的拼法可拼出一个梯形,你能用这个图形的面积证明勾股定理吗?
用两个直角边分别为a,b,斜边为c的全等直角三角形,按如图所示的拼法可拼出一个梯形,你能用这个图形的面积证明勾股定理吗?考点:勾股定理的证明
专题:
分析:用三角形的面积和、梯形的面积来表示这个图形的面积,从而证明勾股定理.
解答:解:三个Rt△其面积分别为
ab,
ab和
c2.
直角梯形的面积为
(a+b)(a+b).
由图形可知:
(a+b)(a+b)=
ab+
ab+
c2
整理得(a+b)2=2ab+c2,a2+b2+2ab=2ab+c2,
∴a2+b2=c2.
由此验证勾股定理.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
直角梯形的面积为
| 1 |
| 2 |
由图形可知:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得(a+b)2=2ab+c2,a2+b2+2ab=2ab+c2,
∴a2+b2=c2.
由此验证勾股定理.
点评:此题主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2证明勾股定理.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
某市为了鼓励居民节约用水,对自来水用户按如下标准收费:若每月每户用水不超过12吨,按每吨a元收费;若超过12吨,则超过部分按每吨2a收费,如果某户居民五月份缴纳水费20a元,则该居民这个月实际用水多少吨?( )
| A、4 | B、8 | C、12 | D、16 |
 如图所示,在△ABD和△ACE中,AB=AC,AD=AE.欲证△ABD≌△ACE,必须补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE.欲证△ABD≌△ACE,必须补充的条件是( )| A、∠B=∠C |
| B、∠D=∠E |
| C、∠BAC=∠DAE |
| D、∠CAD=∠DAE |
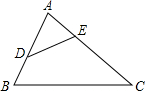 如图,要判断△ADE与△ACB相似,添加一个条件,不正确的是( )
如图,要判断△ADE与△ACB相似,添加一个条件,不正确的是( )| A、∠ADE=∠C |
| B、∠AED=∠B |
| C、AE:DE=AB:BC |
| D、AE:AD=AB:AC. |
在平面直角坐标系中,将点P(1,2)向左平移2个单位长度后得到点Q,则点Q的坐标是( )
| A、(-1,2) |
| B、(3,2) |
| C、(1,4) |
| D、(1,0) |
 如图,由小正方形组成的格点图形,将图中某一个小正方形涂上阴影,与图中的三个阴影部分构成轴对称图形.
如图,由小正方形组成的格点图形,将图中某一个小正方形涂上阴影,与图中的三个阴影部分构成轴对称图形. 如图,已知AB∥CD,CE∥BF.求证:∠B=∠C.
如图,已知AB∥CD,CE∥BF.求证:∠B=∠C. 如图所示,直线AB,CD相交于点O,OE⊥AB,且∠DOE=40°,求∠AOC.
如图所示,直线AB,CD相交于点O,OE⊥AB,且∠DOE=40°,求∠AOC.