题目内容
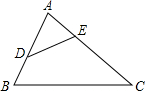如图，要判断△ADE与△ACB相似，添加一个条件，不正确的是（ ）| A、∠ADE=∠C |
| B、∠AED=∠B |
| C、AE：DE=AB：BC |
| D、AE：AD=AB：AC． |
考点：相似三角形的判定
专题：
分析：本题中已知∠A是公共角，应用两三角形相似的判定定理，即可作出判断．
解答：解：由图得：∠A=∠A
∴当∠ADE=∠C或∠ADE=∠B或AE：AD=AB：AC时，△ADE与△ACB相似；
C选项中∠A不是成比例的两边的夹角，不能判定△ADE与△ACB相似．
故选：C．
∴当∠ADE=∠C或∠ADE=∠B或AE：AD=AB：AC时，△ADE与△ACB相似；
C选项中∠A不是成比例的两边的夹角，不能判定△ADE与△ACB相似．
故选：C．
点评：此题考查了相似三角形的判定：
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
练习册系列答案
相关题目
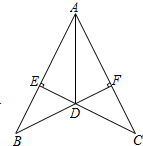如图，BF⊥AC，CE⊥AB，BE=CF，BF与CE相交于点D，则图中的全等三角形有
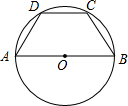如图，四边形ABCD是⊙O的内接四边形，其中AB是⊙O的直径，已知AD=CD，CD∥AB，则∠BCD的度数是
用两个直角边分别为a，b，斜边为c的全等直角三角形，按如图所示的拼法可拼出一个梯形，你能用这个图形的面积证明勾股定理吗？
如图，在△ABC中，∠ACB=90°，点D，E在AB上，且AF垂直平分CD，BG垂直平分CE展览馆有A，B两个入口，D、E、F三个出口，则从A入口进，F出口出的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|