题目内容
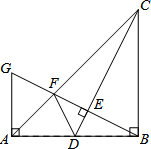 如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①
如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①| AG |
| AB |
| FG |
| FB |
| ||
| 3 |
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:相似三角形的判定与性质,等腰直角三角形
专题:
分析:根据同角的余角相等求出∠ABG=∠BCD,然后利用“角边角”证明△ABC和△BCD全等,根据全等三角形对应边相等可得AG=BD,然后求出AG=
BC,再求出△AFG和△CFB相似,根据相似三角形对应边成比例可得
=
,从而判断出①正确;求出FG=
FB,然后根据FE≠BE判断出②错误;根据相似三角形对应边成比例求出
=
,再根据等腰直角三角形的性质可得AC=
AB,然后整理即可得到AF=
AB,判断出③正确;过点F作MF⊥AB于M,根据三角形的面积整理即可判断出④错误.
| 1 |
| 2 |
| AG |
| AB |
| FG |
| FB |
| 1 |
| 2 |
| AF |
| FC |
| 1 |
| 2 |
| 2 |
| ||
| 3 |
解答:解:∵∠ABC=90°,BG⊥CD,
∴∠ABG+∠CBG=90°,∠BCD+∠CBG=90°,
∴∠ABG=∠BCD,
在△ABC和△BCD中,
,
∴△ABG≌和△BCD(ASA),
∴AG=BD,
∵点D是AB的中点,
∴BD=
AB,
∴AG=
BC,
在Rt△ABC中,∠ABC=90°,
∴AB⊥BC,
∵AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴
=
,
∵BA=BC,
∴
=
,故①正确;
∵△AFG∽△CFB,
∴
=
=
,
∴FG=
FB,
∵FE≠BE,
∴点F是GE的中点不成立,故②错误;
∵△AFG∽△CFB,
∴
=
=
,
∴AF=
AC,
∵AC=
AB,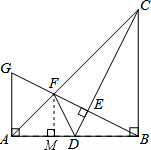
∴AF=
AB,故③正确;
过点F作MF⊥AB于M,则FM∥CB,
∴
=
=
,
∵
=
,
∴
=
=
•
=
•
=
,故④错误.
综上所述,正确的结论有①③共2个.
故选C.
∴∠ABG+∠CBG=90°,∠BCD+∠CBG=90°,
∴∠ABG=∠BCD,
在△ABC和△BCD中,
|
∴△ABG≌和△BCD(ASA),
∴AG=BD,
∵点D是AB的中点,
∴BD=
| 1 |
| 2 |
∴AG=
| 1 |
| 2 |
在Rt△ABC中,∠ABC=90°,
∴AB⊥BC,
∵AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴
| AG |
| CB |
| FG |
| FB |
∵BA=BC,
∴
| AG |
| AB |
| FG |
| FB |
∵△AFG∽△CFB,
∴
| GF |
| BF |
| AG |
| BC |
| 1 |
| 2 |
∴FG=
| 1 |
| 2 |
∵FE≠BE,
∴点F是GE的中点不成立,故②错误;
∵△AFG∽△CFB,
∴
| AF |
| CF |
| AG |
| BC |
| 1 |
| 2 |
∴AF=
| 1 |
| 3 |
∵AC=
| 2 |

∴AF=
| ||
| 3 |
过点F作MF⊥AB于M,则FM∥CB,
∴
| AF |
| AC |
| FM |
| BC |
| 1 |
| 3 |
∵
| BD |
| BA |
| 1 |
| 2 |
∴
| S△BDF |
| S△ABC |
| ||
|
| BD |
| AB |
| FM |
| BC |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
综上所述,正确的结论有①③共2个.
故选C.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形的性质,熟练掌握相似三角形的判定方法和相似三角形对应边成比例的性质是解题的关键.

练习册系列答案
相关题目
若x2-10xy+N是一个完全平方式,那么N是( )
| A、5y2 |
| B、y2 |
| C、100y2 |
| D、25y2 |
 如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=( )
如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=( )| A、150° | B、140° |
| C、130° | D、120° |
 如图,AD∥BC可以得到( )
如图,AD∥BC可以得到( )| A、∠1=∠2 |
| B、∠2=∠3 |
| C、∠1=∠4 |
| D、∠3=∠4 |
已知关于x的方程ax-2=0的解是x=1,则a的值是( )
| A、0 | B、1 | C、2 | D、3 |
 如图所示,?ABCD的对角线AC、BD相交于点O,BD=12cm,点E在线段BO上从点B开始以1cm/s的速度运动,点F在线段OD上从O点开始以2cm/s的速度运动.若点E、F同时运动,且当点F运动到D点时,点E、F同时停止运动,设运动时间为ts,当t为何值时,四边形AECF是平行四边形?
如图所示,?ABCD的对角线AC、BD相交于点O,BD=12cm,点E在线段BO上从点B开始以1cm/s的速度运动,点F在线段OD上从O点开始以2cm/s的速度运动.若点E、F同时运动,且当点F运动到D点时,点E、F同时停止运动,设运动时间为ts,当t为何值时,四边形AECF是平行四边形?