题目内容
 如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=( )
如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=30°,则∠BOC=( )| A、150° | B、140° |
| C、130° | D、120° |
考点:垂线,对顶角、邻补角
专题:
分析:根据垂直的定义可得∠BOE=90°,然后列式计算即可求出∠BOD,再根据邻补角互补求出∠BOC即可.
解答:解:∵EO⊥AB,
∴∠BOE=90°,
∵∠EOD=30°,
∴∠BOD=90°-∠EOD=90°-30°=60°,
∴∠BOC=180°-∠BOD=180°-60°=120°,
故选:D.
∴∠BOE=90°,
∵∠EOD=30°,
∴∠BOD=90°-∠EOD=90°-30°=60°,
∴∠BOC=180°-∠BOD=180°-60°=120°,
故选:D.
点评:本题主要考查了垂线的定义,对顶角相等,邻补角互补的性质,是基础题,准确识图是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 已知抛物线y=a(x-3)2+
已知抛物线y=a(x-3)2+| 25 |
| 4 |
①抛物线的对称轴是直线x=3;
②点C在⊙D外;
③在抛物线上存在一点E,能使四边形ADEC为平行四边形;
④直线CM与⊙D相切.
正确的结论是( )
| A、①③ | B、①④ |
| C、①③④ | D、①②③④ |
有下列各数,0.456,
,3.14,0.80108,
,0.3
,0.101001…,
,其中无理数有( )
| 3π |
| 2 |
| 27 |
| • |
| 6 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,由AC∥ED,可知相等的角有( )
如图,由AC∥ED,可知相等的角有( )| A、6对 | B、5对 | C、4对 | D、3对 |
菱形具有但是平行四边形不具有的性质( )
| A、对角线互相平分 |
| B、邻边相等 |
| C、对角线相等 |
| D、是中心对称图形 |
一个正数的两个平方根分别为a-7和2a+1,则a是( )
| A、-1 | B、-2 | C、1 | D、2 |
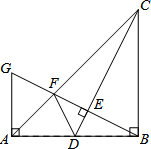 如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①
如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①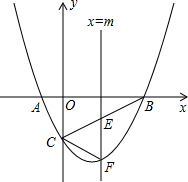 如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于点C,已知A(-1,0),且tan∠ABC=
如图,抛物线y=ax2+bx-2与x轴交于A、B两点,与y轴交于点C,已知A(-1,0),且tan∠ABC=