题目内容
 如图,AD∥BC可以得到( )
如图,AD∥BC可以得到( )| A、∠1=∠2 |
| B、∠2=∠3 |
| C、∠1=∠4 |
| D、∠3=∠4 |
考点:平行线的性质
专题:
分析:此题是AD与BC两条平行线被AC所截,截得的内错角为∠2与∠3,根据平行线的判定定理即可判断.
解答:解:A、∠1=∠2,因为它们不是两平行线被截得的同位角或内错角,故错误;
B、∠2=∠3,是AD和BC被AC所截形成的内错角,根据内错角相等,两直线平行即可判断AD∥BC,故选项正确;
C、∠1和∠4,是AB和CD被AC所截形成的内错角,故不能证明AD∥BC,选项错误;
D、∠3和角5,因为它们不是两平行线被截得的内错角,不符合题意,故错误;
故选B.
B、∠2=∠3,是AD和BC被AC所截形成的内错角,根据内错角相等,两直线平行即可判断AD∥BC,故选项正确;
C、∠1和∠4,是AB和CD被AC所截形成的内错角,故不能证明AD∥BC,选项错误;
D、∠3和角5,因为它们不是两平行线被截得的内错角,不符合题意,故错误;
故选B.
点评:此题考查了平行线的性质:两直线平行,内错角相等.解题的关键是找到截线与被截线.

练习册系列答案
相关题目
一个等腰三角形的两边分别为2cm和5cm,那么它的周长为( )cm.
| A、9 | B、12 |
| C、9或12 | D、以上都不对 |
设A(x1,y1),B(x2,y2)是正比例函数y=-2x图象上的两点,若x1<x2<0,则y1与y2之间的关系是( )
| A、y2<y1<0 |
| B、y1<y2<0 |
| C、y2>y1>0 |
| D、y1>y2>0 |
菱形具有但是平行四边形不具有的性质( )
| A、对角线互相平分 |
| B、邻边相等 |
| C、对角线相等 |
| D、是中心对称图形 |
等边三角形的对称轴有( )条.
| A、1 | B、2 | C、3 | D、4 |
下列命题是真命题的是( )
| A、对顶角相等 |
| B、两直线被第三条直线所截,内错角相等 |
| C、相等的角是对顶角 |
| D、两直线被第三条直线所截,同位角相等 |
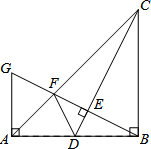 如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①
如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①