题目内容
 如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=6,AB=10,则BD的长是
如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=6,AB=10,则BD的长是考点:平行四边形的性质,勾股定理
专题:
分析:由AC⊥BC,若BC=6,AB=10,根据勾股定理,可求得AC的长,然后由平行四边形的性质以及勾股定理求得BE的长,继而求得答案.
解答:解:∵AC⊥BC,BC=6,AB=10,
∴AC=
=8,
∵四边形ABCD是平行四边形,
∴EC=
AC=4,
∴BE=
=2
,
∴BD=2BE=4
.
故答案为:4
.
∴AC=
| AB2-BC2 |
∵四边形ABCD是平行四边形,
∴EC=
| 1 |
| 2 |
∴BE=
| BC2+EC2 |
| 13 |
∴BD=2BE=4
| 13 |
故答案为:4
| 13 |
点评:此题考查了平行四边形的性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
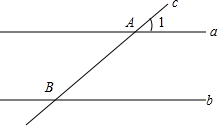 如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.
如图,直线a∥b,直线与直线a、b分别交与点A、B且∠1=45°.
 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是