题目内容
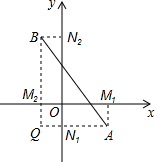 阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,∴AB2=AQ2+BQ2=|x1-x2|+|y1-y2|2=(x1-x2|2+(y1-y2)2,
由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:AB=
| (x1-x2)2+(y1-y2)2 |
(1)直接应用平面内两点间距离公式计算点A(1,-3),B(-2,1)之间的距离为
(2)平面直角坐标系中的两点A(2,3),B(4,1),P为x轴上任一点,则PA+PB的最小值为
(3)应用平面内两点间的距离公式,求代数式
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
考点:轴对称-最短路线问题,两点间的距离公式
专题:阅读型
分析:(1)直接利用两点之间距离公式直接求出即可;
(2)利用轴对称求最短路线方法得出P点位置,进而求出PA+PB的最小值;
(3)根据原式表示的几何意义是点(x,y)到点(-2,-4)和(3,1)的距离之和,当点(x,y)在以(-2,-4)和(3,1)为端点的线段上时其距离之和最小,进而求出即可.
(2)利用轴对称求最短路线方法得出P点位置,进而求出PA+PB的最小值;
(3)根据原式表示的几何意义是点(x,y)到点(-2,-4)和(3,1)的距离之和,当点(x,y)在以(-2,-4)和(3,1)为端点的线段上时其距离之和最小,进而求出即可.
解答:解:(1)∵平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
AB=
,
∴点A(1,-3),B(-2,1)之间的距离为:
=5;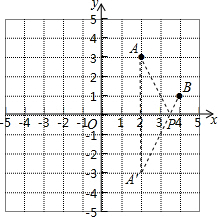
故答案为:5;
(2)如图所示:作A点关于x轴对称点A′点,连接A′B,
则此时PA+PB最小,最小值为:
=2
;
故答案为:2
;
(3)原式表示的几何意义是点(x,y)到点(0,2)和(3,1)的距离之和,
当点(x,y)在以(0,2)和(3,1)为端点的线段上时其距离之和最小,
∴原式最小为
=
.
AB=
| (x1-x2)2+(y1-y2)2 |
∴点A(1,-3),B(-2,1)之间的距离为:
| (1+2)2+(-3-1)2 |

故答案为:5;
(2)如图所示:作A点关于x轴对称点A′点,连接A′B,
则此时PA+PB最小,最小值为:
| 42+22 |
| 5 |
故答案为:2
| 5 |
(3)原式表示的几何意义是点(x,y)到点(0,2)和(3,1)的距离之和,
当点(x,y)在以(0,2)和(3,1)为端点的线段上时其距离之和最小,
∴原式最小为
| (0-3)2+(2-1)2 |
| 10 |
点评:此题主要考查了利用轴对称求最值问题以及两点之间距离公式,正确转化代数式为两点之间距离问题是解题关键.

练习册系列答案
相关题目
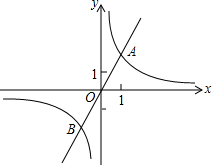 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y= 1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.
1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m. 如图,∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,∠COE的度数是∠AOB的度数的2倍吗?如果是,请说明理由.
如图,∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,∠COE的度数是∠AOB的度数的2倍吗?如果是,请说明理由.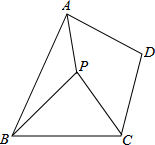 在四边形ABCD中,AB=BC,∠ABC=60°,线段CD绕着点C逆时针旋转60°得到线段CP,连接PA、PB.
在四边形ABCD中,AB=BC,∠ABC=60°,线段CD绕着点C逆时针旋转60°得到线段CP,连接PA、PB.