题目内容
15.若关于x的方程x2+(|k|-2)x+k=0 的两根互为相反数,则k=-2.分析 若方程的两根互为相反数,则两根的和为0;可用含k的代数式表示出两根的和,即可列出关于k的方程,解方程求出k的值,再把所求的k的值代入判别式△进行检验,使△<0的值应舍去.
解答 解:设原方程的两根为x1、x2,则x1+x2=|k|-2=0;
∴k1=2,k2=-2;
∴当k1=2时,x2+2=0,原方程无实根;
∴k=-2.
故答案为:-2.
点评 此题考查了一元二次方程根与系数的关系定理及相反数的定义.能够根据两根互为相反数的条件列出关于k的方程,是解答此题的关键;注意根与系数的关系定理适用的条件是判别式△≥0,这是本题容易出错的地方.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
6.如果点A(-2,a),B(b,1)是反比例函数y=-$\frac{6}{x}$图象上的两点,那么a,b的值分别是( )
| A. | 3,6 | B. | -3,6 | C. | 3,-6 | D. | -3,-6 |
5.下列运算中没有意义的是( )
| A. | -2006÷[(-$\frac{7}{3}$)×3+7] | B. | [(-$\frac{7}{3}$)×3+7]÷(-2006) | C. | ($\frac{1}{3}$-$\frac{1}{2}$)÷[0-(-4)]×(-2) | D. | 2$\frac{1}{3}$÷(3$\frac{1}{3}$×6-18) |
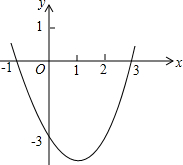 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: 已知△ABC和△ADE都是等腰直角三角形,如图摆放使得一直角边重合,连接BD,CE.问:BD和CE有何位置关系?并给出证明.
已知△ABC和△ADE都是等腰直角三角形,如图摆放使得一直角边重合,连接BD,CE.问:BD和CE有何位置关系?并给出证明. 已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.
已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.