题目内容
10. 已知△ABC和△ADE都是等腰直角三角形,如图摆放使得一直角边重合,连接BD,CE.问:BD和CE有何位置关系?并给出证明.
已知△ABC和△ADE都是等腰直角三角形,如图摆放使得一直角边重合,连接BD,CE.问:BD和CE有何位置关系?并给出证明.
分析 已知△ABC和△ADE都是等腰直角三角形从而得到两腰相等,两直角相等,从而可以利用SAS判定△ABD≌△ACE,从而得出BD=CE.
解答 解:BD=CE,理由如下:
∵△ABC和△ADE都是等腰直角三角形
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAC=∠DAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=CE.
点评 此题主要考查全等三角形的判定方法,常用的判定方法有AAS、SAS、SSS、ASA、HL等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知AB=CD,AD=BC,BE=DF.求证:∠E=∠F.
已知AB=CD,AD=BC,BE=DF.求证:∠E=∠F. 如图,M是线段AB的中点,点C在线段AB上,N是AC的中点,且AN=2cm,CM=1cm,求线段AB的长.
如图,M是线段AB的中点,点C在线段AB上,N是AC的中点,且AN=2cm,CM=1cm,求线段AB的长. 如图,正五边形ABCDE的中心为O,边心距OH=1,AF,AG分别垂直于CB,DE,且分别交它们的延长线于点F,G.求OA+FA+GA的值.
如图,正五边形ABCDE的中心为O,边心距OH=1,AF,AG分别垂直于CB,DE,且分别交它们的延长线于点F,G.求OA+FA+GA的值.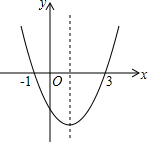 如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )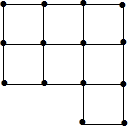 如图所示是由20根小棒摆成的大小相同的7个正方形,很明显它不是轴对称图形,请你将一根小棒移动到合适的位置,使移动后的图形成为一个轴对称图形.
如图所示是由20根小棒摆成的大小相同的7个正方形,很明显它不是轴对称图形,请你将一根小棒移动到合适的位置,使移动后的图形成为一个轴对称图形.