题目内容
11.在函数y=x2□4x□4的空格中,任意填上“+”或“-”,可组成若干个不同的二次函数,其中其图象的顶点在x轴上的概率为$\frac{1}{2}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与其图象的顶点在x轴上的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有4种等可能的结果,其中其图象的顶点在x轴上的有(+,+),(-,+),
∴其图象的顶点在x轴上的概率为:$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
14.下列各式计算正确的是( )
| A. | a2+3a2=4a4 | B. | 3a3•2a2=6a6 | C. | a5÷a=a4 | D. | -2-2=$\frac{1}{4}$ |
3.当k为何值时,25x2-kxy+49y2是一个完全平方式( )
| A. | -35 | B. | -70 | C. | ±35 | D. | ±70 |
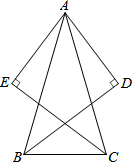 如图,△ABC为等腰三角形,AB=AC,BD分别平分∠ABC,CE分别平分∠ACB,过点A分别作BD、CE的垂线段,垂足为D、E.求证:AD=AE.
如图,△ABC为等腰三角形,AB=AC,BD分别平分∠ABC,CE分别平分∠ACB,过点A分别作BD、CE的垂线段,垂足为D、E.求证:AD=AE.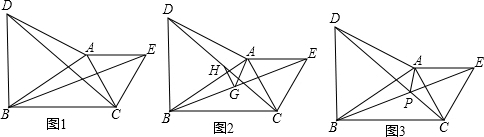
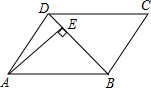 如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E.则∠DAE为20度.
如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E.则∠DAE为20度.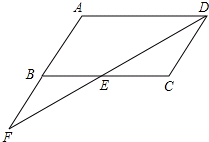 已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.
已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.