题目内容
20.已知关于x的方程x2-(3k-1)x+2k(k-1)=0.(1)求证:无论k为何实数,方程总有实数根.
(2)若此方程有两个实数根x1,x2,且(x1-x2)2=4,求k的值.
分析 (1)确定判别式的范围即可得出结论;
(2)根据根与系数的关系表示出x1+x2,x1x2,继而根据题意得出方程,解出即可.
解答 (1)证明:∵方程x2-(3k-1)x+2k(k-1)=0是一元二次方程,
∴△=(3k-1)2-4×2k(k-1)=(k+1)2≥0,
∴无论k为任何实数,方程总有实数根.
(2)解:∵此方程有两个实数根x1,x2,
∴x1+x2=3k-1,x1x2=2k(k-1),
∵(x1-x2)2=4,
∴(x1+x2)2-4x1x2=4,
即(3k-1)2-4×2k(k-1)=4,
解得:k=1或k=-3.
点评 本题主要考查一元二次方程根的判别式和根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
10.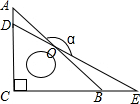 把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
 把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )| A. | 165° | B. | 135° | C. | 115° | D. | 95° |
11.下列图形中既是中心对称又是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 角 | D. | 菱形 |
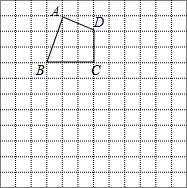 作图题:(不要求写作法)如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上)
作图题:(不要求写作法)如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上) 如图,矩形ABCD中,AB=7,AD=5,点E在CD上,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的平分线上时,点D′到AB的距离是3或4.
如图,矩形ABCD中,AB=7,AD=5,点E在CD上,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的平分线上时,点D′到AB的距离是3或4.