题目内容
15.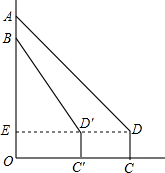 星期天,小华到小明家邀请小明到新华书店看书,当小华到达CD(点D是小华的眼睛)处时,发现小明在七楼A处,此时测得仰角为45°,继续向前走了10m到达C′D′处,发现小明在六楼B处,此时测得仰角为60°,已知楼层高AB=2.7m,求OC′的长.(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
星期天,小华到小明家邀请小明到新华书店看书,当小华到达CD(点D是小华的眼睛)处时,发现小明在七楼A处,此时测得仰角为45°,继续向前走了10m到达C′D′处,发现小明在六楼B处,此时测得仰角为60°,已知楼层高AB=2.7m,求OC′的长.(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
分析 连接DD′并延长交OA于E,则DE⊥OA,先解Rt△ADE,得AE=DE,在Rt△BD′E中,得BE=$\sqrt{3}$D′E,即10+D′E=BE+2.7,从而求求出D′E的值即可.
解答 解:连接DD′,并延长交AO于点E,则DE⊥OA,
在Rt△ADE中,∵∠AED=90°,∠ADE=45°,
∴AE=DE,
在Rt△BD′E中,∵∠BED′=90°,∠BD′E=60°,
∴BE=$\sqrt{3}$D′E.
∴10+D′E=BE+2.7
解得D′E=10m,
∴OC′=10m.
答:OC′的长为10m.
点评 此题主要考查了解直角三角形的应用,解题的关键是从题目中整理出直角三角形并正确的利用边角关系求解.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
5.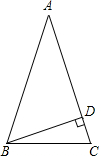 如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
 如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )| A. | 36° | B. | 30° | C. | 24° | D. | 18° |
3.如图,用围棋子按下面的规律摆图形,则摆第10个图形需要围棋子的枚数是( )
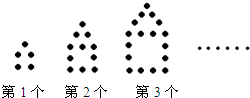

| A. | 50 | B. | 54 | C. | 59 | D. | 65 |
10.下列方程的解是x=1的是( )
| A. | $\frac{x-1}{2}$=10 | B. | 2-x=2x-1 | C. | $\frac{2}{x}$+1=0 | D. | x2=2 |
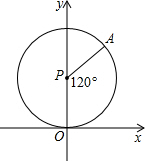 如图,⊙P与x轴切于点O,点P(0,1)在y轴上,点A在⊙P上,并且在第一象限,∠APO=120°.⊙P沿x轴正方向滚动,当点A第一次落在x轴上时为点A′,则点A′的坐标为($\frac{2π}{3}$,0)(结果保留π).
如图,⊙P与x轴切于点O,点P(0,1)在y轴上,点A在⊙P上,并且在第一象限,∠APO=120°.⊙P沿x轴正方向滚动,当点A第一次落在x轴上时为点A′,则点A′的坐标为($\frac{2π}{3}$,0)(结果保留π).
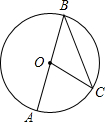 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B=40°.
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B=40°.