题目内容
若分式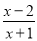 的值为0,则x的值为( )
的值为0,则x的值为( )
A. -1 B. 0 C. 2 D. -1或2
 C
【解析】因为分式的值为0,所以,解得,故选C.
C
【解析】因为分式的值为0,所以,解得,故选C.
练习册系列答案
相关题目
对于平面直角坐标系中任意两点M(x1, y1),N(x2,y2),称|x1﹣x2|+|y1﹣y2|为M,N两点的勾股距离,记作:d(M,N).如:M(2,﹣3),N(1,4),则d(M,N)=|2-1|+|-3-4|=8. 若P(x0,y0)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P,Q)的最小值为P到直线y=kx+b的勾股距离.则P(-3,2)到直线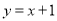 的勾股距离为( )
的勾股距离为( )
A. 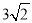 B.
B. 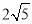 C. 3 D. 4
C. 3 D. 4
 D
【解析】根据垂线段最短,可得当PQ直线时,PQ最短,设PQ 的解析式为y=-x+b,把P(-3,2)代入求得b=-1,所以PQ 的解析式为y=-x-1,令-x-1=x+1,解得x=-1.把x=-1代入y=x+1得y=0,即可得点Q的坐标为(-1,0),所以P(-3,2)到直线的勾股距离为|-3﹣(-1))|+|2﹣0|=2+2=4,故选D.
D
【解析】根据垂线段最短,可得当PQ直线时,PQ最短,设PQ 的解析式为y=-x+b,把P(-3,2)代入求得b=-1,所以PQ 的解析式为y=-x-1,令-x-1=x+1,解得x=-1.把x=-1代入y=x+1得y=0,即可得点Q的坐标为(-1,0),所以P(-3,2)到直线的勾股距离为|-3﹣(-1))|+|2﹣0|=2+2=4,故选D. 当a=2016时,分式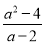 的值是_____.
的值是_____.
 2018
【解析】 = =a+2,
把a=2016代入得:
原式=2016+2=2018.
故答案为:2018.
2018
【解析】 = =a+2,
把a=2016代入得:
原式=2016+2=2018.
故答案为:2018. 若关于x的方程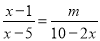 无解,则m=___________.
无解,则m=___________.
 -8 .
【解析】试题分析:去分母可得:x-1=-,解得:x=1-,根据分式无解可知x=5,即1-=5,解得:m=-8.
-8 .
【解析】试题分析:去分母可得:x-1=-,解得:x=1-,根据分式无解可知x=5,即1-=5,解得:m=-8. 若x=-1,y=2,则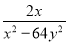 -
-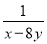 的值为( )
的值为( )
A. -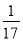 B.
B. 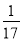 C.
C. 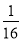 D.
D. 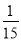
 D
【解析】试题分析:原式====,
当, 时,原式==.故选D.
D
【解析】试题分析:原式====,
当, 时,原式==.故选D. 如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.试说明:点E,F关于AD对称.
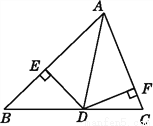
 见解析
【解析】试题分析:连接EF交AD于点G,根据已知条件易证AE=AF,DE=DF,即可得AD垂直平分EF,从而结论得证.
试题解析:
如图,连接EF交AD于点G,
因为AD平分∠BAC,所以∠EAD=∠FAD.
又因为∠AED=∠AFD,AD=AD,
所以Rt△ADE≌Rt△ADF(AAS).
所以AE=AF,DE=DF.
所以AD垂直平分EF...
见解析
【解析】试题分析:连接EF交AD于点G,根据已知条件易证AE=AF,DE=DF,即可得AD垂直平分EF,从而结论得证.
试题解析:
如图,连接EF交AD于点G,
因为AD平分∠BAC,所以∠EAD=∠FAD.
又因为∠AED=∠AFD,AD=AD,
所以Rt△ADE≌Rt△ADF(AAS).
所以AE=AF,DE=DF.
所以AD垂直平分EF... 如图,在矩形ABCD中,AB=10,BC=5点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为【 】
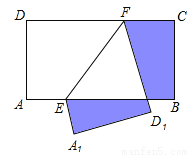
A.15 B.20 C.25 D.30
 D
【解析】翻折变换(折叠问题),矩形和折叠的性质。
根据矩形和折叠的性质,得A1E=AE,A1D1=AD,D1F=DF,则阴影部分的周长即为矩形的周长,为2(10+5)=30。故选D。
D
【解析】翻折变换(折叠问题),矩形和折叠的性质。
根据矩形和折叠的性质,得A1E=AE,A1D1=AD,D1F=DF,则阴影部分的周长即为矩形的周长,为2(10+5)=30。故选D。 

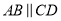 ,
, 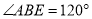 ,
, 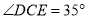 ,则
,则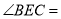 __________.
__________.