题目内容
3.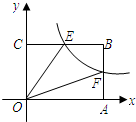 如图,y=$\frac{k}{x}$(x>0)经过矩形的边AB、BC的中点F、E,四边形OEBF的面积为2,则k=2.
如图,y=$\frac{k}{x}$(x>0)经过矩形的边AB、BC的中点F、E,四边形OEBF的面积为2,则k=2.
分析 设F(a,$\frac{k}{a}$),则B(a,$\frac{2k}{a}$),则E($\frac{1}{2}$a,$\frac{2k}{a}$),根据反比例函数的比例系数k的几何意义,利用S矩形OCBA-S△OAF-S△OEC=S四边形OEFB得到a•$\frac{2k}{a}$-$\frac{1}{2}$k-$\frac{1}{2}$k=2,解得k=2.
解答 解:设F(a,$\frac{k}{a}$),则B(a,$\frac{2k}{a}$),则E($\frac{1}{2}$a,$\frac{2k}{a}$),
∵四边形OEBF的面积为2,
∴S矩形OCBA-S△OAF-S△OEC=S四边形OEFB,
即a•$\frac{2k}{a}$-$\frac{1}{2}$k-$\frac{1}{2}$k=2,
∴k=2.
故答案为2.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.下列分式中,是最简分式的是( )
| A. | $\frac{2a}{3{a}^{2}b}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{a}^{2}+ab}{ab+{b}^{2}}$ |
 如图所示是某战役缴获敌军防御工事坐标地图的碎片,依稀可见:一号暗堡A的坐标为(4,3),五号暗堡B的坐标为(-2,3),另有情报得知敌军指挥部的坐标为(-3,-2).请你在图中画出直角坐标系,并且标示出敌军指挥部的位置.
如图所示是某战役缴获敌军防御工事坐标地图的碎片,依稀可见:一号暗堡A的坐标为(4,3),五号暗堡B的坐标为(-2,3),另有情报得知敌军指挥部的坐标为(-3,-2).请你在图中画出直角坐标系,并且标示出敌军指挥部的位置.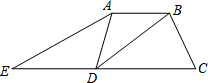 如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.
如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.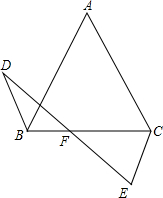 如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.
如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.