Question

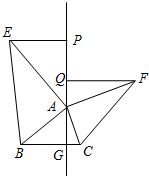已知，如图，在△ABC中，AG⊥BC于G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作Rt△ABE和Rt△ACF，分别过点E、F作射线GA的垂线，垂足分别为P、Q．
（1）若PE=4，AP=5，BG=3，求线段AG的长；
（2）若AB=kAE，AC=kAF（k＞0），求线段EP与线段FQ的数量关系．

Answer 1

考点：相似三角形的判定与性质,全等三角形的判定与性质

专题：

分析：（1）易证△AEP∽△BAG，可求得AG的长；
（2）通过相似三角形△AEP∽△BAG的对应边成比例知：

EP

AG

=

AE

AB

=

1

k

，则易证△FQA∽△AGC，所以

FQ

AG

=

AF

AC

=

1

k

．故EP=FQ．

解答：解：（1）∵∠EAP+∠PEA=90°，∠BAG+∠EAP=90°，
∴∠PEA=∠BAG，
∴△AEP∽△BAG，
∴

PE

AG

=

AP

BG

，AG=

12

5

，
（2）∵EP⊥AG，AG⊥BC，
∴∠EPA=∠BGA=90°．
又∵∠EAB=90°，
∴∠PEA=∠GAB，∠PAE=∠GBA（同角的余角相等），
∴△AEP∽△BAG，
∴

EP

AG

=

AE

AB

=

1

k

（相似三角形的对应边成比例），
同理，△FQA∽△AGC，则

FQ

AG

=

AF

AC

=

1

k

（相似三角形的对应边成比例），
∴

EP

AG

=

FQ

AG

（等量代换），
∴EP=FQ．

点评：本题考查了相似综合题．其中涉及到的知识点有矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质等，利用比例相等也可以证明线段相等．