题目内容
已知在梯形ABCD中，AB∥CD，对角线AC、BD交于O点，S△AOD：S△DOC=2：3，求S△AOB：S△DOC．
考点：梯形,相似三角形的判定与性质
专题：
分析：由于AB∥CD，根据三角形相似的判定方法得到△ODC∽△OBA，根据三角形相似的性质得到S△ODC：S△AOB=OC2：OA2=1：4，则OC：OA=1：2，然后根据同高的两三角形面积的比等于底边的比求解．
解答：解：如图所示：
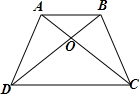
∵S△AOD：S△DOC=2：3，
∴AO：OC=2：3，
∵AB∥CD，
∴∠OAB=∠OCD，∠ABO=∠CDO，
∴△ODC∽△OBA，
∴S△AOB：S△DOC=OA2：OC2=4：9．
∵S△AOD：S△DOC=2：3，
∴AO：OC=2：3，
∵AB∥CD，
∴∠OAB=∠OCD，∠ABO=∠CDO，
∴△ODC∽△OBA，
∴S△AOB：S△DOC=OA2：OC2=4：9．
点评：本题考查了梯形的性质、相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截的三角形与原三角形相似；相似三角形面积的比等于相似比的平方．也考查了三角形的面积公式．
练习册系列答案
相关题目
如图，AB是⊙O1的直径，AO1是⊙O2的直径，弦MN∥AB，且MN与⊙O2相切于点C，若⊙O1的半径为2．阴影部分的面积=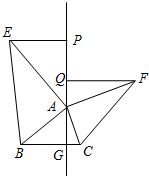
已知，如图，在△ABC中，AG⊥BC于G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作Rt△ABE和Rt△ACF，分别过点E、F作射线GA的垂线，垂足分别为P、Q．
请你先自编写出一组12个数，然后再填入图中恰当的位置，使每个正方形四个顶点处的“○”中的数的和都为-6．
如图，A、B、C在一条直线上，△ABD和△BCE都是等边三角形，则图中通过旋转能够互相重合的三角形共有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |
如图：A、D、F、B在同一直线上，AD=BF，AE=BC，且AE∥DC．