如图.有一条圆形拱桥.拱的跨度AB=303.拱的半径R=30.则拱形的高度等于．题目和参考答案——青夏教育精英家教网—

题目内容

如图，有一条圆形拱桥，拱的跨度AB=30

，拱的半径R=30，则拱形的高度等于

．

考点：垂径定理的应用,勾股定理

专题：

分析：过O作OD⊥AB，交AB于点C，交

于点D，如图所示，利用垂径定理得到C为AB的中点，由AB长求出AC长，在直角三角形AOC中根据勾股定理求出OC的长，进而可得出CD的长．

解答：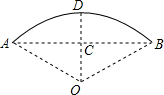

解：解：过O作OD⊥AB，交AB于点C，交

于点D，如图所示，
∴C为AB的中点，即AC=BC=

AB=15

．
在Rt△AOC中，
∵AC=15

m，OA=30，
∴OC=

OA2-AC2

302-(15

=15，
∴CD=OD-OC=30-15=15．
故答案为：15．

点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．

练习册系列答案

相关题目

计算：（-1001）²⁰⁰⁹×（0.125）²⁰⁰⁸×（-

）²⁰⁰⁹×（-

）²⁰⁰⁹．[注：aⁿbⁿ=（ab）ⁿ]．

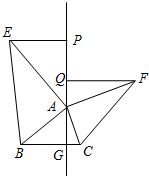已知，如图，在△ABC中，AG⊥BC于G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作Rt△ABE和Rt△ACF，分别过点E、F作射线GA的垂线，垂足分别为P、Q．
（1）若PE=4，AP=5，BG=3，求线段AG的长；
（2）若AB=kAE，AC=kAF（k＞0），求线段EP与线段FQ的数量关系．

请你先自编写出一组12个数，然后再填入图中恰当的位置，使每个正方形四个顶点处的“○”中的数的和都为-6．

根据下面给出的数轴，解答下面的问题：
（1）观察数轴，与点A的距离为3的点表示的数是：

；
（2）若将数轴折叠，使得A点与-3表示的点重合，则B点与数

表示的点重合；
（3）若数轴上M、N两点之间的距离为2014（M在N的右侧），且M、N两点经过（3）中折叠后互相重合，则M、N两点表示的数分别是：M：

N：

．

如图，A、B、C在一条直线上，△ABD和△BCE都是等边三角形，则图中通过旋转能够互相重合的三角形共有（　　）

3	-8

．5，-3，π
（2）将上面几个数用“＜”连结起来：

试题分类