题目内容
3.定义:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数.如:2的差倒数是$\frac{1}{1-2}=-1$,-1的差倒数是$\frac{1}{{1-({-1})}}=\frac{1}{2}$.已知a1=-3,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2011=-3.分析 根据差倒数的定义分别求出前几个数便不难发现,每3个数为一个循环组依次循环,用2011除以3,根据余数的情况确定出与a2011相同的数即可得解.
解答 解:∵a1=-3,
∴a2=$\frac{1}{1-(-3)}$=$\frac{1}{4}$,
a3=$\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$,
a4=$\frac{1}{1-\frac{4}{3}}$=-3,
…
2011÷3=670…1.
∴a2011与a1相同为-3.
故答案为:-3.
点评 本题是对数字变化规律的考查,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.

练习册系列答案
相关题目
13. 如图,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B=( )
如图,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B=( )
 如图,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B=( )
如图,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B=( )| A. | 36° | B. | 45° | C. | 72° | D. | 30° |
15. 一个正方体的每个面都有一个汉字,其平面展开图如图所示,该正方体中和“乐”相对的字是( )
一个正方体的每个面都有一个汉字,其平面展开图如图所示,该正方体中和“乐”相对的字是( )
 一个正方体的每个面都有一个汉字,其平面展开图如图所示,该正方体中和“乐”相对的字是( )
一个正方体的每个面都有一个汉字,其平面展开图如图所示,该正方体中和“乐”相对的字是( )| A. | 学 | B. | 习 | C. | 我 | D. | 快 |
13.把分式$\frac{x^2}{x-y}$中的x和y的值都扩大到原来的2倍,则分式的值为( )
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 扩大为原来的4倍 | D. | 缩小为原来的$\frac{1}{2}$ |
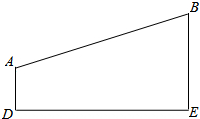 如图,已知AD⊥DE,BE⊥DE,∠DAB与∠ABE的平分线交于C点.
如图,已知AD⊥DE,BE⊥DE,∠DAB与∠ABE的平分线交于C点.
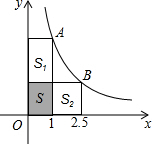 如图,A、B两点在双曲线y=$\frac{k}{x}$(x>0)的图象上,已知点$A(1,4),B(\frac{5}{2},m)$,分别经过A、B两点向坐标轴作垂线段,得到三个矩形:记阴影部分矩形面积为S,另两个矩形面积分别记为S1、S2.
如图,A、B两点在双曲线y=$\frac{k}{x}$(x>0)的图象上,已知点$A(1,4),B(\frac{5}{2},m)$,分别经过A、B两点向坐标轴作垂线段,得到三个矩形:记阴影部分矩形面积为S,另两个矩形面积分别记为S1、S2.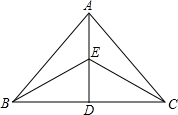 如图△ABC中,D点是BC上的点,E是AD的中点,△BCE的面积是1,则△ABC的面积是( )
如图△ABC中,D点是BC上的点,E是AD的中点,△BCE的面积是1,则△ABC的面积是( )