题目内容
已知关于x方程2x2+kx-1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是
,求另一个根及k的值.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是
| 1 |
| 2 |
考点:根的判别式,根与系数的关系
专题:
分析:(1)要证明方程有两个不相等的实数根,即证明△>0即可.△=k2-4×2×(-1)=k2+8,因为k2≥0,可以得到△>0,从而得出答案.
(2)把方程的一根代入原方程求出k的值,然后把k的值代入原方程求出方程的另一个根.
(2)把方程的一根代入原方程求出k的值,然后把k的值代入原方程求出方程的另一个根.
解答:解:(1)∵△=k2-4×2×(-1)=k2+8,
又∵k2≥0,
∴k2+8>0,
∴△>0;
∴方程有两个不相等的实数根;
(2)把x=
代入方程得:
+
k-1=0,
解得k=1,
把k=1代入方程得:2x2+x-1=0,
解得:x1=
,x2=-1,
则k的值为1,方程的另一个根为-1.
又∵k2≥0,
∴k2+8>0,
∴△>0;
∴方程有两个不相等的实数根;
(2)把x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得k=1,
把k=1代入方程得:2x2+x-1=0,
解得:x1=
| 1 |
| 2 |
则k的值为1,方程的另一个根为-1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
小明到商店为自己和弟弟各买一套相同的衣服,甲、乙两个商店的每套衣服售价相同,甲店的优惠数是:若一次买两套则其中一套可获得7折优惠;乙店的优惠数是:若一次买两套,则享受总价的8折优惠,你认为( )
| A、甲店比乙店优惠 |
| B、乙店比甲店优惠 |
| C、甲、乙两家都一样 |
| D、以上都有可能 |
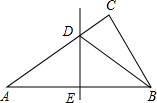 如图,在△ABC中,∠C=90°,DE垂直平分AB,交AC于点D,交AB于点E,若∠A=35°.求∠CBD的度数.
如图,在△ABC中,∠C=90°,DE垂直平分AB,交AC于点D,交AB于点E,若∠A=35°.求∠CBD的度数.