题目内容
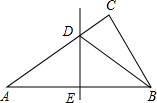如图，在△ABC中，∠C=90°，DE垂直平分AB，交AC于点D，交AB于点E，若∠A=35°．求∠CBD的度数．考点：线段垂直平分线的性质
专题：
分析：由三角形内角和定理求出∠ABC=55°，又由DE垂直平分AC推出DA=DB，推出∠A=∠ABD=35°，即可得出答案．
解答：解：∵∠C=90°，∠A=35°，
∴∠ABC=55°，
∵DE垂直平分AB
∴DA=DB，
∴∠A=∠DBA=35°
∴∠CBD=∠ABC-∠ABD=45°-35°=10°．
∴∠ABC=55°，
∵DE垂直平分AB
∴DA=DB，
∴∠A=∠DBA=35°
∴∠CBD=∠ABC-∠ABD=45°-35°=10°．
点评：此题考查了线段垂直平分线的性质，等腰三角形性质，三角形内角和定理的应用，解题的关键是注意数形结合思想的应用，注意等量代换思想的应用．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图，△ABC中，AB=18，AC=16，D在AB上，AD=9，在AC上取一点P，问AP=