题目内容
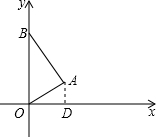如图所示，∠BAO=90°，OA=| 1 |
| 2 |
考点：含30度角的直角三角形,坐标与图形性质
专题：
分析：如图，过点A作AE⊥OB于点E．利用“等角的余角相等”推知∠ABE=∠EAO=30°，通过解图中的两个直角三角形来求BE的长度，则BO的长度迎刃而解，易求点B的坐标．
解答：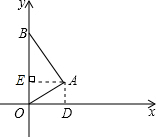
解：如图，过点A作AE⊥OB于点E．
∵∠BAO=90°，
∴∠ABE=∠EAO（等角的余角相等）．
又∵OA=
OB，
∴∠ABE=∠EAO=30°，
∴AE=OE•cot30°=2×
=
，
∴BE=AE•cot30°=
×
=
，
∴OB=OE+BE=2+
=
．
∴点B的坐标是（0，
）．
故答案是：（0，
）．
解：如图，过点A作AE⊥OB于点E．∵∠BAO=90°，
∴∠ABE=∠EAO（等角的余角相等）．
又∵OA=
| 1 |
| 2 |
∴∠ABE=∠EAO=30°，
∴AE=OE•cot30°=2×
| ||
| 3 |
2
| ||
| 3 |
∴BE=AE•cot30°=
2
| ||
| 3 |
| ||
| 3 |
| 2 |
| 3 |
∴OB=OE+BE=2+
| 2 |
| 3 |
| 8 |
| 3 |
∴点B的坐标是（0，
| 8 |
| 3 |
故答案是：（0，
| 8 |
| 3 |
点评：本题考查了含30度的直角三角形和坐标与图形的性质．此题也可以利用勾股定理进行解答相关线段的长度．
练习册系列答案
相关题目
已知一元二次方程的两根分别是2和1，则这个一元二次方程是（ ）
| A、x2-3x+2=0 |
| B、x2+3x-2=0 |
| C、x2-2x+3=0 |
| D、x2+3x+2=0 |
实数-
，0，
，-2π，
，0.1010001000001…（两个1之间依次多两个0）中，无理数的个数有（ ）
| 8 |
| 7 |
| 6 |
| 3 | -125 |
| A、3个 | B、4个 | C、5个 | D、6个 |
作图题 
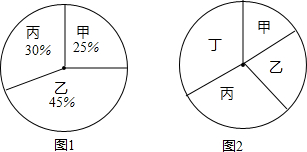分别求出每个扇形的圆心角的度数．
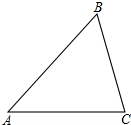（1）如图，在锐角△ABC中，利用三角函数的定义及勾股定理证明你的猜想；