题目内容
已知一元二次方程的两根分别是2和1，则这个一元二次方程是（ ）
| A、x2-3x+2=0 |
| B、x2+3x-2=0 |
| C、x2-2x+3=0 |
| D、x2+3x+2=0 |
考点：根与系数的关系
专题：
分析：利用一元二次方程的根与系数之间的关系可知：用两根x1，x2表示的一元二次方程的形式为：x2-（x1+x2）x+x1•x2=0．把对应数值代入即可求解．
解答：解：设这样的方程为x2+bx+c=0，
则根据根与系数的关系，可得：
b=-（2+1）=-3，c=2×1=2；
所以方程是x2-3x+2=0．
故选A．
则根据根与系数的关系，可得：
b=-（2+1）=-3，c=2×1=2；
所以方程是x2-3x+2=0．
故选A．
点评：本题考查了一元二次方程根与系数的关系，比较简单．要求掌握根与系数的关系：x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
，x1x2=
，反过来也成立，即
=-（x1+x2），
=x1x2．以两个数x1，x2为根的一元二次方程可表示为：x2-（x1+x2）x+x1•x2=0．
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
如图是计算机程序计算图．下列计算正确的是（ ）
A、
| |||
B、
| |||
C、
| |||
D、
|
已知x，y为实数，且
+3（y-2）2=0，则（x，y）在第（ ）象限．
| x-1 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列变形中正确的是（ ）
| A、x2-（-x+y）=x2+x-y |
| B、3a-（b+c-d）=3a-b+c-d |
| C、4+2（a-b）=4+2a-b |
| D、a+（b-c）=ab-c |
下列说法中，错误的是（ ）
| A、a2-b2表示的是a的平方与b的平方的差 | ||
| B、5（a+b）表示的是a与b的和的5倍 | ||
| C、比x的2倍少3的数，用代数式表示为2x-3 | ||
D、x的5倍与y的和的一半，用代数式表示为5x+
|
若|x+
|+（2y+1）2=0，则x2+y2的值是（ ）
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、
| ||
| D、1 |
某商品的单件售价为a元，经过二次降价，每次降价x%，则两次降价后的售价为（ ）元．
| A、a（1-x%）2 |
| B、a（1+x%）2 |
| C、a-（x%）2 |
| D、（1-x%）2 |
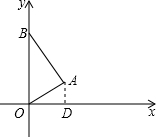如图所示，∠BAO=90°，OA=