题目内容
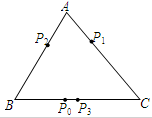 某种“电子爬虫“游戏盘是如图所示的三角形形状,其中AB=6,AC=7,BC=8,爬虫沿游戏盘的边BC、CA、AB按逆时针方向运动.如果爬虫开始时在BC边的P0处,BP0=2.爬虫第一步从P0爬到AC边的P1(第一次落点处),且CP1=CP0;第二步从P1爬到AB边的P2(第二次落点)处,且AP2=AP1;第三步从P2爬到BC边的P3(第三次落点)处,且BP3=BP2;…;爬虫按上述规则一直跳下去,第n次落点Pn(n为正整数),则点P5与P2012之间的距离为
某种“电子爬虫“游戏盘是如图所示的三角形形状,其中AB=6,AC=7,BC=8,爬虫沿游戏盘的边BC、CA、AB按逆时针方向运动.如果爬虫开始时在BC边的P0处,BP0=2.爬虫第一步从P0爬到AC边的P1(第一次落点处),且CP1=CP0;第二步从P1爬到AB边的P2(第二次落点)处,且AP2=AP1;第三步从P2爬到BC边的P3(第三次落点)处,且BP3=BP2;…;爬虫按上述规则一直跳下去,第n次落点Pn(n为正整数),则点P5与P2012之间的距离为考点:规律型:图形的变化类
专题:
分析:根据跳蚤的运动轨迹,找出从每一步跳动后的位置,进而得出P6点与P0点重合,得出P2012点与P2点和P5点重合,进而解答即可.
解答:解:根据规律:CP1=CP0=8-2=6,
AP1=AP2=7-6=1,
BP2=BP3=6-1=5,
CP3=CP4=8-5=3,
AP4=AP5=7-3=4,
…
由此可得
P0P3=CP0-CP3=6-3=3,
P1P4=AP4-AP1=4-1=3,
P2P5=AP5-AP2=4-1=3,
…
由此可知,P6点与P0点重合,P5点与P2点重合,又因为2012=6×335+2,
所以P2012点与P2点重合,
∴点P5与P2012之间的距离为:P5P2015=0.
故答案为:0.
AP1=AP2=7-6=1,
BP2=BP3=6-1=5,
CP3=CP4=8-5=3,
AP4=AP5=7-3=4,
…
由此可得
P0P3=CP0-CP3=6-3=3,
P1P4=AP4-AP1=4-1=3,
P2P5=AP5-AP2=4-1=3,
…
由此可知,P6点与P0点重合,P5点与P2点重合,又因为2012=6×335+2,
所以P2012点与P2点重合,
∴点P5与P2012之间的距离为:P5P2015=0.
故答案为:0.
点评:此题主要考查了规律型中点的坐标变化,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,得出P2012点与P2点重合是解题关键.

练习册系列答案
相关题目
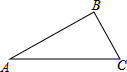 如图△ABC是一个直三棱柱的俯视图,若该直三棱柱的高10cm,∠A=30°,∠C=45°,BC=2
如图△ABC是一个直三棱柱的俯视图,若该直三棱柱的高10cm,∠A=30°,∠C=45°,BC=2| 2 |
A、(42+22
| ||||
B、(22+42
| ||||
C、(44+24
| ||||
D、(60+20
|
若x<y成立,则下列不等式成立的是( )
| A、x-2<y-2 |
| B、-x<-y |
| C、x+1>y+1 |
| D、-3x<-3y |
在-
,0,-|-5|,-0.
,2,
,-10中负数的个数有( )
| 7 |
| 10 |
| • |
| 6 |
| 1 |
| 3 |
| A、3 | B、4 | C、5 | D、6 |
下列命题的逆命题不正确的是( )
| A、直角三角形中斜边上的中线等于斜边的一半 |
| B、两直线平行,内错角相等 |
| C、等腰三角形的两个底角相等 |
| D、对顶角相等 |