题目内容
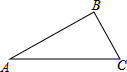 如图△ABC是一个直三棱柱的俯视图,若该直三棱柱的高10cm,∠A=30°,∠C=45°,BC=2
如图△ABC是一个直三棱柱的俯视图,若该直三棱柱的高10cm,∠A=30°,∠C=45°,BC=2| 2 |
A、(42+22
| ||||
B、(22+42
| ||||
C、(44+24
| ||||
D、(60+20
|
考点:解直角三角形,简单几何体的三视图
专题:
分析:该直三棱柱的主视图与左视图都是矩形,俯视图是三角形,根据矩形与三角形的面积公式分别计算,再相加即可.
解答: 解:过B作BD⊥AC于D.
解:过B作BD⊥AC于D.
在Rt△BCD中,∵∠BDC=90°,∠C=45°,BC=2
cm,
∴BD=CD=
BC=2cm,
在Rt△BAD中,∵∠BDA=90°,∠A=30°,
∴AB=2BD=4cm,AD=
BD=2
cm,
∴AC=AD+CD=(2
+2)cm.
主视图的面积是:10(2
+2)=20
+20(cm2),
左视图的面积是:10×2=20(cm2),
俯视图的面积是:
×(2
+2)×2=2
+2(cm2),
∴该直三棱柱的三种视图的面积之和为:20
+20+20+2
+2=42+22
(cm2).
故选A.
 解:过B作BD⊥AC于D.
解:过B作BD⊥AC于D.在Rt△BCD中,∵∠BDC=90°,∠C=45°,BC=2
| 2 |
∴BD=CD=
| ||
| 2 |
在Rt△BAD中,∵∠BDA=90°,∠A=30°,
∴AB=2BD=4cm,AD=
| 3 |
| 3 |
∴AC=AD+CD=(2
| 3 |
主视图的面积是:10(2
| 3 |
| 3 |
左视图的面积是:10×2=20(cm2),
俯视图的面积是:
| 1 |
| 2 |
| 3 |
| 3 |
∴该直三棱柱的三种视图的面积之和为:20
| 3 |
| 3 |
| 3 |
故选A.
点评:本题考查了解直角三角形,简单几何体的三视图,得出该直三棱柱的三种视图的形状是解题的关键.

练习册系列答案
相关题目
 如图是一个表面带有图案的正方体,则其表面展开图可能是( )
如图是一个表面带有图案的正方体,则其表面展开图可能是( )A、 |
B、 |
C、 |
D、 |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,令x0=
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,令x0=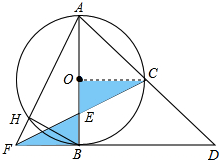 如图,以AB为直径的⊙O切△AFD的边FD于点B,AD交⊙O于点C,且C是弧AB的中点,CF交AB于点E,且E为OB中点.若AF交⊙O于点H,连接BH,若OA=4,求BH的长.
如图,以AB为直径的⊙O切△AFD的边FD于点B,AD交⊙O于点C,且C是弧AB的中点,CF交AB于点E,且E为OB中点.若AF交⊙O于点H,连接BH,若OA=4,求BH的长.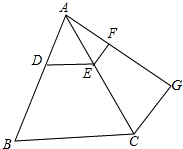 如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.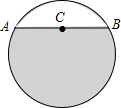 某居民区一处圆形下水管道破裂需要更换,下水管道横截面如图所示,已知污水面宽AB=60m,C为AB中点,且C点距管道底部的距离为90cm,求圆形管道的直径.
某居民区一处圆形下水管道破裂需要更换,下水管道横截面如图所示,已知污水面宽AB=60m,C为AB中点,且C点距管道底部的距离为90cm,求圆形管道的直径.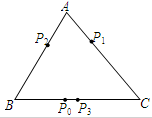 某种“电子爬虫“游戏盘是如图所示的三角形形状,其中AB=6,AC=7,BC=8,爬虫沿游戏盘的边BC、CA、AB按逆时针方向运动.如果爬虫开始时在BC边的P0处,BP0=2.爬虫第一步从P0爬到AC边的P1(第一次落点处),且CP1=CP0;第二步从P1爬到AB边的P2(第二次落点)处,且AP2=AP1;第三步从P2爬到BC边的P3(第三次落点)处,且BP3=BP2;…;爬虫按上述规则一直跳下去,第n次落点Pn(n为正整数),则点P5与P2012之间的距离为
某种“电子爬虫“游戏盘是如图所示的三角形形状,其中AB=6,AC=7,BC=8,爬虫沿游戏盘的边BC、CA、AB按逆时针方向运动.如果爬虫开始时在BC边的P0处,BP0=2.爬虫第一步从P0爬到AC边的P1(第一次落点处),且CP1=CP0;第二步从P1爬到AB边的P2(第二次落点)处,且AP2=AP1;第三步从P2爬到BC边的P3(第三次落点)处,且BP3=BP2;…;爬虫按上述规则一直跳下去,第n次落点Pn(n为正整数),则点P5与P2012之间的距离为