Question

12．在四边形ABCD中，AC=AB，DC=DB，∠CAB=60°，∠CDB=120°，E是AC上一点，F是AB延长线上一点，且CE=BF． 
（1）请判断DE=DF吗？说出你的理由； 
（2）若点G在AB上，且∠EDG=60°，是猜想CE、EG、BG之间的数量关系，并说明理由．

Answer 1

分析 （1）通过角的计算得出∠C=∠DBF，结合CD=BD、CE=BF即可证出△CDE≌△BDF（SAS），由此即可得出DE=DF；
（2）连接AD，结合AC=AB、DC=DB即可证出△ABD≌△ACD（SSS），由此即可得出∠BDA=∠CDA=60°，再根据∠EDG=60°即可得出∠CDE=∠ADG，∠ADE=∠BDG，由（1）可知△CDE≌△BDF，进而得知∠CDE=∠BDF，根据角的计算即可得出∠EDG=∠FDG，结合DE=DF即可证出△DEG≌△DFG（SAS），即得出EG=FG，由相等的边与边之间的关系即可证出CE+BG=EG．

解答 解：（1）DE=DF．理由如下：
∵∠CAB+∠C+∠CDB+∠ABD=360°，∠CAB=60°，∠CDB=120°，
∴∠C+∠ABD=360°-60°-120°=180°．
又∵∠DBF+∠ABD=180°，
∴∠C=∠DBF．
在△CDE和△BDF中，$\left\{\begin{array}{l}{CD=BD}\\{∠C=∠DBF}\\{CE=BF}\end{array}\right.$，
∴△CDE≌△BDF（SAS）．
∴DE=DF．
（2）猜想CE、EG、BG之间的数量关系为：CE+BG=EG．理由如下：
 连接AD，如图所示．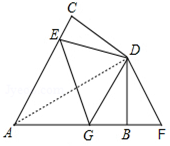
 在△ABD和△ACD中，$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$，
∴△ABD≌△ACD（SSS），
∴∠BDA=∠CDA=$\frac{1}{2}$∠CDB=$\frac{1}{2}$×120°=60°．
又∵∠EDG=60°，
∴∠CDE=∠ADG，∠ADE=∠BDG．
由（1）可得：△CDE≌△BDF，
∴∠CDE=∠BDF．
∴∠BDG+∠BDF=60°，即∠FDG=60°．
∴∠EDG=∠FDG．
在△DEG和△DFG中，$\left\{\begin{array}{l}{ED=FD}\\{∠EDG=∠FDG}\\{DG=DG}\end{array}\right.$，
∴△DEG≌△DFG（SAS），
∴EG=FG．
又∵CE=BF，FG=BF+BG，
∴CE+BG=EG．

点评 本题考查了全等三角形的判定与性质以及角的计算，解题的关键是：（1）证出△CDE≌△BDF；（2）证出EG=FG．本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边角关系是关键．