题目内容
8.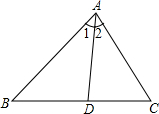 己知:如图所示,∠1=∠2,AB>AC,求证:BD>DC.
己知:如图所示,∠1=∠2,AB>AC,求证:BD>DC.
分析 过C作CE∥AB交AD的延长线于E,根据平行线的性质得到∠E=∠1,由已知条件得到∠2=∠E,于是得到CE=AC,通过△CDE∽△ABD,得到比例是$\frac{AB}{CE}=\frac{BD}{CD}$,即$\frac{AB}{BD}=\frac{AC}{CD}$=k,于是得到kBD>kCD,即可得到结论.
解答 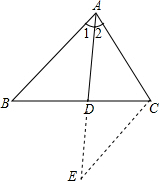 解:过C作CE∥AB交AD的延长线于E,
解:过C作CE∥AB交AD的延长线于E,
∴∠E=∠1,
∵∠1=∠2,
∴∠2=∠E,
∴CE=AC,
∵CE∥AB,
∴△CDE∽△ABD,
∴$\frac{AB}{CE}=\frac{BD}{CD}$,
∴$\frac{AB}{AC}=\frac{BD}{CD}$,
即$\frac{AB}{BD}=\frac{AC}{CD}$=k,
∴AB=kBD,AC=kCD,
∵AB>AC,
∴kBD>kCD,
∴BD>DC.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,比例的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目