题目内容
20.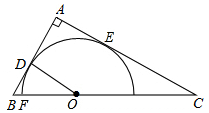 如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=4,AE=6,tan∠BOD=$\frac{2}{3}$.
如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=4,AE=6,tan∠BOD=$\frac{2}{3}$.(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线.
分析 (1)由AC为圆O的切线,利用切线的性质得到OD垂直于AC,在直角三角形ADO中,利用锐角三角函数定义,根据tan∠AOD及AD的值,求出OD的值即可;
(2)连接OE,由CE=OD=3,且OD与AE平行,利用一组对边平行且相等的四边形为平行四边形,根据平行四边形的对边平行得到OE与AD平行,再由DA与AE垂直得到OE与AC垂直,即可得证.
解答 解:(1)∵AB与圆O相切,
∴OD⊥AB
在Rt△BDO中,BD=4,tan∠BOD=$\frac{BD}{OD}$=$\frac{2}{3}$,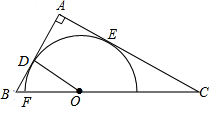
∴OD=6;
(2)连接OE,
∵AE=OD=6,AE∥OD,
∴四边形AEOD为平行四边形,
∴AD∥EO,
∵DA⊥AE,
∴OE⊥AC,
又∵OE为圆的半径,
∴AC为圆O的切线;
点评 此题考查了切线的判定与性质,锐角三角函数定义,平行四边形的判定与性质,以及平行线的性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
11. 在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
 在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )| A. | a | B. | 2b | C. | 2a-2b | D. | -2b |
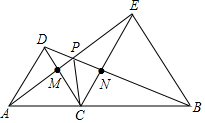 如图,△DAC和△EBC均是等边三角形,AE交BD于P点,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③∠APD=60°;④∠APC=60°,其中正确个数是( )
如图,△DAC和△EBC均是等边三角形,AE交BD于P点,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③∠APD=60°;④∠APC=60°,其中正确个数是( )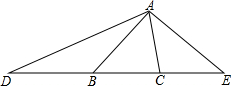 如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
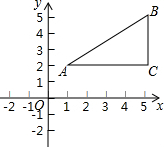 如图,在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E(点E不与点B重合),使△ACE和△ACB全等,写出所有满足条件的E点的坐标E1(5,-1),E2(1,-1),E3(1,5).
如图,在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E(点E不与点B重合),使△ACE和△ACB全等,写出所有满足条件的E点的坐标E1(5,-1),E2(1,-1),E3(1,5).