题目内容
 已知点A(4,0)及在第一象限的动点P(x,y),且x+y=6,设△OPA的面积为S.
已知点A(4,0)及在第一象限的动点P(x,y),且x+y=6,设△OPA的面积为S.(1)求S关于x的函数关系式,并写出自变量x的取值范围;
(2)求S=10时P点坐标;
(3)在(2)的基础上,设点Q为y轴上一动点,当PQ+AQ的值最小时,求Q点坐标.
考点:一次函数综合题
专题:
分析:(1)首先把x+y=6,变形成y=6-x,再利用三角形的面积求法:底×高÷2=S,可以得到S关于x的函数表达式;P在第一象限,故x>0,再利用三角形的面积S>0,可得到x的取值范围;
(2)把S=10代入函数解析式即可;
(3)根据题意画出图象,作出A的对称点A′,连接PA′,此时PA′与y轴交于点Q,此时PQ+AQ的值最小,进而求出即可.
(2)把S=10代入函数解析式即可;
(3)根据题意画出图象,作出A的对称点A′,连接PA′,此时PA′与y轴交于点Q,此时PQ+AQ的值最小,进而求出即可.
解答:解:(1)∵x+y=6,
∴y=6-x,
∴S=4(6-x)÷2=12-2x,
∵12-2x>0,
∴x<6,
∴0<x<6,
(2)∵s=10,
∴10=12-2x,
解得:x=1,
∴y=6-1=5,
∴s=10时,P点坐标(1,5);
(3)如图所示.
作出A的对称点A′,连接PA′,此时PA′与y轴交于点Q,此时PQ+AQ的值最小,
∵A点坐标为(4,0),
∴A′(-4,0),
∴将(-4,0),(1,5)代入y=kx+b,
∴
,
解得:
,
∴y=x+4,
∴x=0时,y=4,
当PQ+AQ的值最小时,Q点坐标为:(0,4).
∴y=6-x,
∴S=4(6-x)÷2=12-2x,
∵12-2x>0,
∴x<6,
∴0<x<6,
(2)∵s=10,

∴10=12-2x,
解得:x=1,
∴y=6-1=5,
∴s=10时,P点坐标(1,5);
(3)如图所示.
作出A的对称点A′,连接PA′,此时PA′与y轴交于点Q,此时PQ+AQ的值最小,
∵A点坐标为(4,0),
∴A′(-4,0),
∴将(-4,0),(1,5)代入y=kx+b,
∴
|
解得:
|
∴y=x+4,
∴x=0时,y=4,
当PQ+AQ的值最小时,Q点坐标为:(0,4).
点评:此题主要考查了待定系数法求函数解析式以及画一次函数的图象和最短路线求法,解题时一定要注意自变量的取值范围.

练习册系列答案
相关题目
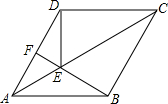 如图,点E是菱形ABCD对角线AC上的一点,连接BE,DE.
如图,点E是菱形ABCD对角线AC上的一点,连接BE,DE. 如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF.
如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF.
 (1)一个角的补角与它余角的2倍的差是平角
(1)一个角的补角与它余角的2倍的差是平角 将圆柱形纸筒的侧面沿虚线剪开,得到的平面图形是
将圆柱形纸筒的侧面沿虚线剪开,得到的平面图形是 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB; ②CM=CN;③AC=DN; ④PC平分∠APB; ⑤∠APD=60°.其中不正确结论是
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB; ②CM=CN;③AC=DN; ④PC平分∠APB; ⑤∠APD=60°.其中不正确结论是