题目内容
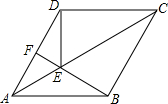 如图,点E是菱形ABCD对角线AC上的一点,连接BE,DE.
如图,点E是菱形ABCD对角线AC上的一点,连接BE,DE.(1)求证:△AEB≌△AED;
(2)延长BE交AD于点F,若DE⊥CD于点D,且sin∠ADE=
| 1 |
| 2 |
①求证:BF⊥AD.
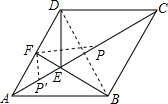
②若EF=1,点P为线段AC上一动点,设AP=a,试问:当a为何值时,△AFP与△ADE相似?
考点:菱形的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)利用菱形的性质得出DE=BE,进而得出△AEB≌△AED;
(2)①利用平行线的性质以及全等三角形的性质得出∠DAB+∠ABF=90°,进而得出答案;
②利用分类讨论得出当△AFP′∽△ADE时,当△AFP∽△AED时,分别求出即可.
(2)①利用平行线的性质以及全等三角形的性质得出∠DAB+∠ABF=90°,进而得出答案;
②利用分类讨论得出当△AFP′∽△ADE时,当△AFP∽△AED时,分别求出即可.
解答:(1)证明:连接BD,
∵E是菱形ABCD对角线AC上的一点,
∴AC垂直平分BD,则DE=BE,
在△AEB和△AED中
,
∴△AEB≌△AED;
(2)①证明:∵DE⊥CD于点D,
∴∠ADE+∠DAB=180°-90°=90°,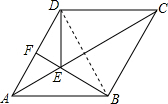
∵△AEB≌△AED,
∴∠ABF=∠ADE,
∴∠DAB+∠ABF=90°,
∴BF⊥AD;
②∵sin∠ADE=
,EF=1,∠DFE=90°,
∴DE=BE=2,∠ADE=30°,
∴∠DAB=60°,
∴DF=AF=
AD=
,
当△AFP∽△AED时,
=
,
∴
=
,
解得:AP=4,
当△AFP′∽△ADE时,
=
,
∴
=
,
解得:AP′=1,
综上所述:当a为1或4时,△AFP与△ADE相似.
∵E是菱形ABCD对角线AC上的一点,
∴AC垂直平分BD,则DE=BE,
在△AEB和△AED中
|
∴△AEB≌△AED;
(2)①证明:∵DE⊥CD于点D,
∴∠ADE+∠DAB=180°-90°=90°,

∵△AEB≌△AED,
∴∠ABF=∠ADE,
∴∠DAB+∠ABF=90°,
∴BF⊥AD;
②∵sin∠ADE=
| 1 |
| 2 |
∴DE=BE=2,∠ADE=30°,
∴∠DAB=60°,
∴DF=AF=
| 1 |
| 2 |
| 3 |
当△AFP∽△AED时,

| AF |
| AE |
| AD |
| AP |
∴
| ||
| 2 |
2
| ||
| AP |
解得:AP=4,
当△AFP′∽△ADE时,
| AP′ |
| AE |
| AF |
| AD |
∴
| AP′ |
| 2 |
| ||||
|
解得:AP′=1,
综上所述:当a为1或4时,△AFP与△ADE相似.
点评:此题主要考查了相似三角形的性质和判定以及菱形的性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 画出图中的物体的三种视图.
画出图中的物体的三种视图.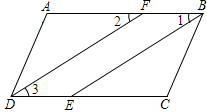 已知,如图,∠ADC=∠ABC,BE,DF分别平分∠ABC,∠ADC,∠1=∠2.求证:∠A=∠C.
已知,如图,∠ADC=∠ABC,BE,DF分别平分∠ABC,∠ADC,∠1=∠2.求证:∠A=∠C. 已知点A(4,0)及在第一象限的动点P(x,y),且x+y=6,设△OPA的面积为S.
已知点A(4,0)及在第一象限的动点P(x,y),且x+y=6,设△OPA的面积为S.