题目内容
 (1)一个角的补角与它余角的2倍的差是平角
(1)一个角的补角与它余角的2倍的差是平角| 1 |
| 3 |
(2)已知:BC∥EF,∠B=∠E,求证:AB∥DE.
考点:平行线的判定与性质,余角和补角
专题:证明题
分析:(1)设这个角的度数为x,根据余角和补角的定义得到180°-x-2(90°-x)=
×180°,然后解方程即可;
(2)由BC∥EF,根据平行线的性质得∠DPC=∠E,而∠B=∠E,所以∠B=∠DPC,然后根据平行线的判定即可得到结论.
| 1 |
| 3 |
(2)由BC∥EF,根据平行线的性质得∠DPC=∠E,而∠B=∠E,所以∠B=∠DPC,然后根据平行线的判定即可得到结论.
解答:(1)解:设这个角的度数为x,
根据题意得180°-x-2(90°-x)=
×180°,
解得x=60°,
即这个角的度数为60°;
(2)证明:∵BC∥EF,
∴∠DPC=∠E,
∵∠B=∠E,
∴∠B=∠DPC,
∴AB∥DE.
根据题意得180°-x-2(90°-x)=
| 1 |
| 3 |
解得x=60°,
即这个角的度数为60°;
(2)证明:∵BC∥EF,
∴∠DPC=∠E,
∵∠B=∠E,
∴∠B=∠DPC,
∴AB∥DE.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;两直线平行,同位角相等.也考查了余角和补角.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
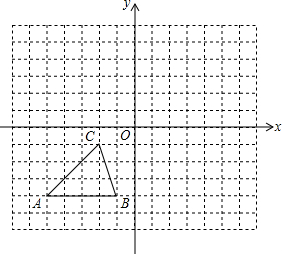 如图,方格纸中的每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫格点.已知△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为l2.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫格点.已知△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为l2. 已知点A(4,0)及在第一象限的动点P(x,y),且x+y=6,设△OPA的面积为S.
已知点A(4,0)及在第一象限的动点P(x,y),且x+y=6,设△OPA的面积为S.