题目内容
12. 如图,AB是⊙O的直径,CD为弦,CD⊥AB且交于点E,则下列结论中不成立的是( )
如图,AB是⊙O的直径,CD为弦,CD⊥AB且交于点E,则下列结论中不成立的是( )| A. | ∠A=∠D | B. | $\widehat{CB}=\widehat{BD}$ | C. | ∠ACB=90° | D. | ∠COB=3∠D |
分析 根据圆周角定理和圆心角、弧、弦之间的关系定理进行判断即可.
解答 解:由圆周角定理得,∠A=∠D成立,A不合题意;
∵∠A=∠D,
∴$\widehat{CB}$=$\widehat{BD}$成立,B不合题意;
∵AB是⊙O的直径,
∴∠ACB=90°正确,C不合题意;
∵∠COB=2∠A,∠A=∠D,
∴∠COB=2∠D,D不成立.
故选:D.
点评 本题考查的是垂径定理和圆周角定理的应用,掌握同弧所对的圆周角相等、直径所对的圆周角是90°是解题的关键.

练习册系列答案
相关题目
2.使分式$\frac{x+2}{{{x^2}+4}}$等于0的x值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 不存在 |
20.如图,以下四个图形是由立体图形展开得到的,相应的立体图形的顺次是( )

| A. | 正方体、圆柱、圆锥、三棱锥 | B. | 正方体、三棱锥、圆柱、圆锥 | ||
| C. | 正方体、圆柱、三棱柱、圆锥 | D. | 三棱锥、圆锥、正方体、圆锥 |

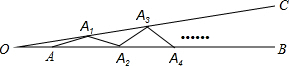 如图,∠BOC=8°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值是( )
如图,∠BOC=8°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值是( ) 如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOE=140°,∠BOC比∠COD的2倍还多10°,那么∠AOB是多少度?
如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOE=140°,∠BOC比∠COD的2倍还多10°,那么∠AOB是多少度?