��Ŀ����
4��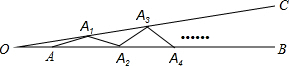 ��ͼ����BOC=8�㣬��A��OB�ϣ���OA=1��������Ҫ��ͼ����AΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A1���õ�1���߶�AA1������A1ΪԲ�ģ�1Ϊ�뾶���һ�����OB�ڵ�A2���õ�2���߶�A1A2������A2ΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A3���õ�3���߶�A2A3������������ȥ��ֱ���õ�n���߶Σ�֮��Ͳ����ٻ�������Ҫ����߶��ˣ���n��ֵ�ǣ�������
��ͼ����BOC=8�㣬��A��OB�ϣ���OA=1��������Ҫ��ͼ����AΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A1���õ�1���߶�AA1������A1ΪԲ�ģ�1Ϊ�뾶���һ�����OB�ڵ�A2���õ�2���߶�A1A2������A2ΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A3���õ�3���߶�A2A3������������ȥ��ֱ���õ�n���߶Σ�֮��Ͳ����ٻ�������Ҫ����߶��ˣ���n��ֵ�ǣ�������| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
���� ���ݵ��������ε����ʺ���������ǵ��������οɵá�A1AA2�Ķ�������A2A1A3�Ķ�������A3A2A4�Ķ�������A4A3A5�Ķ������������˵õ����ɣ��ٸ��ݡ�Ak+1AkAk+2��90�㼴����⣮
��� �⣺�������֪��AO=A1A��A1A=A2A1������
���AOA1=��OA1A����A1AA2=��A1A2A������
�ߡ�BOC=8�㣬
���A1AA2=��2��8���㣬��A2A1A3=��3��8���㣬��A3A2A4=��4��8���㣬��A4A3A5=��5��8���㣬������Ak+1AkAk+2=[��k+2��•8]��
�����⣨k+2��•8��90��
���k��$\frac{37}{4}$��
����kΪ��������k=9�����Ի�11���߶Σ�n=11��
��ѡC��
���� ���⿼���˵��������ε����ʡ������ε�һ����ǵ��ں��������ڵ������ڽǵĺ͵�֪ʶ�����ݹ����г�����ʽ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
14����x���㣨������ʱ�����θ�ʽ$\sqrt{1-x}$��ʵ����Χ�������壮
| A�� | x��1 | B�� | x��1 | C�� | x��1 | D�� | x��1 |
15�� ��ͼ����֪��ABC���DEF�ֱ��ǵȱ������κ͵���ֱ�������Σ�AD��FC�ֱ��ǡ�ABC�͡�DEF�ĸߣ�AC��DF���ڵ�G��BC��DE��ͬһ��ֱ���ϣ�������˵������ȷ���ǣ�������
��ͼ����֪��ABC���DEF�ֱ��ǵȱ������κ͵���ֱ�������Σ�AD��FC�ֱ��ǡ�ABC�͡�DEF�ĸߣ�AC��DF���ڵ�G��BC��DE��ͬһ��ֱ���ϣ�������˵������ȷ���ǣ�������
 ��ͼ����֪��ABC���DEF�ֱ��ǵȱ������κ͵���ֱ�������Σ�AD��FC�ֱ��ǡ�ABC�͡�DEF�ĸߣ�AC��DF���ڵ�G��BC��DE��ͬһ��ֱ���ϣ�������˵������ȷ���ǣ�������
��ͼ����֪��ABC���DEF�ֱ��ǵȱ������κ͵���ֱ�������Σ�AD��FC�ֱ��ǡ�ABC�͡�DEF�ĸߣ�AC��DF���ڵ�G��BC��DE��ͬһ��ֱ���ϣ�������˵������ȷ���ǣ�������| A�� | ��AGD�ס�CGF | B�� | ��AGD�ס�DGC | C�� | $\frac{{S}_{��AGD}}{{S}_{��CGF}}$=3 | D�� | $\frac{AG}{CG}$=$\sqrt{3}$ |
12�� ��ͼ��AB�ǡ�O��ֱ����CDΪ�ң�CD��AB�ҽ��ڵ�E�������н����в��������ǣ�������
��ͼ��AB�ǡ�O��ֱ����CDΪ�ң�CD��AB�ҽ��ڵ�E�������н����в��������ǣ�������
 ��ͼ��AB�ǡ�O��ֱ����CDΪ�ң�CD��AB�ҽ��ڵ�E�������н����в��������ǣ�������
��ͼ��AB�ǡ�O��ֱ����CDΪ�ң�CD��AB�ҽ��ڵ�E�������н����в��������ǣ�������| A�� | ��A=��D | B�� | $\widehat{CB}=\widehat{BD}$ | C�� | ��ACB=90�� | D�� | ��COB=3��D |
19��������2��3��x��4��ƽ������3�����������ݵ������ǣ�������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | ���϶����� |
 ��ͼ����AOB����DOC����ֱ�ǣ�
��ͼ����AOB����DOC����ֱ�ǣ�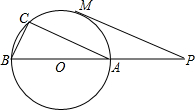 ��ͼ��ֱ��PO����O��A��B���㣬ֱ��AB=10����AC��PM����M��$\widehat{AC}$���е㣬
��ͼ��ֱ��PO����O��A��B���㣬ֱ��AB=10����AC��PM����M��$\widehat{AC}$���е㣬