题目内容
8.问题探究(1)如图1,点E为矩形ABCD内一点,请过点E作一条直线,将矩形ABCD的面积分为相等的两部分;
(2)如图2,在矩形ABCD中,AB=8,BC=6,P为对角线AC上一点,且AC=3AP,请问在边CD上是否存在一点E,使得直线PE将矩形ABCD的面积分为2:3两部分,如果存在求出DE的长;如果不存在,请说明理由;
解决问题
(3)如图3,现有一块矩形空地ABCD,AB=80米,BC=60米,P为对角线AC上一点,且PC=3AP,计划在这块空地上修建一个四边形花园AECF,使得E、F分别在线段AD、AB上,且EF经过点P,若每平方米的造价为100元,请求出修建该花园所需费用的范围(其他费用不计).
分析 (1)连接AC、BD交于点O,作直线EO,直线EO将矩形ABCD的面积分为相等的两部分.
(2)如图2中,作MN∥BC,使得四边形BCMN的面积=$\frac{1}{5}$四边形ABCD的面积,连接AM、DN交于点O,作直线OP交CD于E,交AB于H,此时四边形ADEH的面积:四边形BCEH的面积=2:3.易知CM=BN=$\frac{8}{5}$,DM=AN=$\frac{32}{5}$,由△EOM≌△HAO,得到AH=EM,设AH=EM=x,由AH∥EC,推出$\frac{AH}{EC}$=$\frac{AP}{PC}$=$\frac{1}{2}$,即$\frac{x}{x+\frac{8}{5}}$=$\frac{1}{2}$,解得x=$\frac{8}{5}$,根据DE=DM-EM即可解决问题.
(3)如图3中,连接BD交AC于O,作OM⊥AD于M,ON⊥AN于N.想办法求出四边形AECF的面积的最大值和最小值即可解决问题.
解答 解:(1)如图1中,
连接AC、BD交于点O,作直线EO,直线EO将矩形ABCD的面积分为相等的两部分.
理由:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠MCO=∠NAO,
在△MCO和△NAO中,
$\left\{\begin{array}{l}{∠MCO=∠NAO}\\{∠COM=∠AON}\\{OC=OA}\end{array}\right.$,
△MCO≌△NAO,
∴S△MCO=S△NAO,
∵S△ADC=S△ABC,
∴S四边形ANMD=S四边形BCMN.
(2)如图2中,作MN∥BC,使得四边形BCMN的面积=$\frac{1}{5}$四边形ABCD的面积,
连接AM、DN交于点O,作直线OP交CD于E,交AB于H,此时四边形ADEH的面积:四边形BCEH的面积=2:3.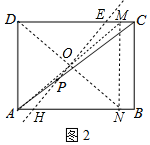
易知:CM=BN=$\frac{8}{5}$,DM=AN=$\frac{32}{5}$,
由△EOM≌△HAO,得到AH=EM,设AH=EM=x,
∵AH∥EC,
∴$\frac{AH}{EC}$=$\frac{AP}{PC}$=$\frac{1}{2}$,
∴$\frac{x}{x+\frac{8}{5}}$=$\frac{1}{2}$,
解得x=$\frac{8}{5}$,
∴DE=DM-EM=$\frac{32}{5}$-$\frac{8}{5}$=$\frac{24}{5}$.
(3)如图3中,连接BD交AC于O,作OM⊥AD于M,ON⊥AN于N.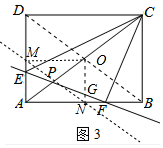
∵PC=3AP,OA=OC,
∴OP=OA,
∴过点P的任意直线将矩形ANOM的面积平分,
∵PC=3AP,
∴S△EPC=3S△EAP,
S△PCF=3S△APF,
∴S四边形AECF=4S△AEF,
当直线EF与对角线MN重合时,△AEF的面积最小(△AEF的面积=$\frac{1}{2}$矩形AMON的面积+△FNG的面积,所以△AEF的面积>△AMN的面积),最小值=$\frac{1}{2}$矩形AMON的面积=600m2,
∴四边形AECF的面积的最小值为2400m2,
当点F与点B重合时,△NGF的面积最大,此时AE=$\frac{1}{3}$BC=20,
∴此时△AEF的面积最大,最大面积=$\frac{1}{2}$×80×20=800m2,
四边形AECF的面积的最大值为3200m2,
∵每平方米的造价为100元
∴修建该花园所需费用w的范围为240000元≤w≤320000元.
点评 本题考查四边形综合题、矩形的性质、平行四边形的性质、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,用转化的思想思考问题,记住平行四边形是中心对称图形,过对称中心的任意直线平分平行四边形的面积,属于中考压轴题.

| A. | 一定是正数 | B. | 可能是正数,也可能是负数 | ||
| C. | 一定是负数 | D. | 不可能是负数 |
| A. | $\left\{\begin{array}{l}{xy=\frac{1}{6}}\\{x+y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x-2y=3}\\{\frac{1}{x}+y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{z=\frac{1}{5}}\\{\frac{x}{2}+\frac{y}{3}=7}\end{array}\right.$ |
| A. | -1 | B. | 0 | C. | -2 | D. | 1 |
①y=10x-9;
②y=-0.3x+2;
③y=$\sqrt{5}$x+4;
④y=($\sqrt{2}$-$\sqrt{3}$)x;
⑤y=7-$\frac{1}{2}$x;
⑥y=8+($\sqrt{5}$-2)x.
| A. | ①③⑥ | B. | ②⑤⑥ | C. | ④⑤⑥ | D. | ②④⑤ |
| A. |  | B. |  | C. |  | D. |  |
| A. | 6a3b=3a2•2ab | B. | t2-3t-10=(t+2)(t-5) | ||
| C. | a2-b2+1=(a+b)(a-b)+1 | D. | (x+y)2=x2+2xy+y2 |
| A. | $\sqrt{12}$×$\sqrt{6}$=6$\sqrt{2}$ | B. | $\sqrt{63}$-$\sqrt{28}$=$\sqrt{7}$ | C. | $\sqrt{17}$÷$\sqrt{85}$×$\sqrt{5}$=1 | D. | ($\sqrt{3}$-$\sqrt{2}$)2=1 |