题目内容
6.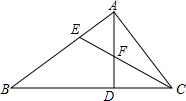 如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.
如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.
分析 根据三角形的内角和定理,可得∠ACB的度数,根据角平分线的定义,可得∠ECB的度数,根据三角形外角的性质,可得∠AEC的度数;根据直角三角形的性质,可得∠CFD的度数,根据对顶角的性质,可得答案.
解答 解:由三角形的内角和定理,得
∠ACB=180°-∠B-∠BAC=180°-40°-80°=60°;
由CE是△ABC的角平分线,得
∠BCE=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×60°=30°,
由∠AEC是△BCE的外角,得
∠AEC=∠B+∠BCE=40°+30°=70°;
由AD⊥BC,得
∠FDC=90°,
∠CFD=90°-∠FCD=90°-30°=60°,
由对顶角相等,得
∠AFE=∠CFD=60°.
点评 本题考查了三角形内角和定理,利用了三角形的内角和定理,三角形外角的性质,直角三角形的性质.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
1.已知D、E分别是△ABC的边AB和AC的中点,F、G分别是AD、AE的中点,若△ABC的面积为16cm2,则四边形DEGF的面积为( )
| A. | 5cm2 | B. | 4cm2 | C. | 3cm2 | D. | 2cm2 |
 如图,△ABC中,AB=AC,∠BAC=90°,且EC⊥AC,EC=AD,求证:AE⊥BD.
如图,△ABC中,AB=AC,∠BAC=90°,且EC⊥AC,EC=AD,求证:AE⊥BD.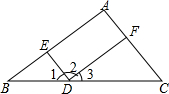 如图,推理填空:
如图,推理填空: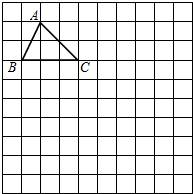 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′′顺时针旋转90°,得到△A′′B′′C′′,请你画出△A′′B′′C′′和△A′′B′′C′′(不要求写画法).
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′′顺时针旋转90°,得到△A′′B′′C′′,请你画出△A′′B′′C′′和△A′′B′′C′′(不要求写画法).