题目内容
15.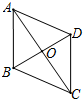 如图,菱形ABCD的对角线AC与BD交于点O,AC=16,BD=12,则边长AB为10,周长为40.
如图,菱形ABCD的对角线AC与BD交于点O,AC=16,BD=12,则边长AB为10,周长为40.
分析 根据菱形的对角线互相垂直平分,可知AO和BO的长,再根据勾股定理即可求得AB的值,又菱形的四条边相等,继而求出菱形的周长.
解答 解:∵AC=16,BD=12,菱形对角线互相垂直平分,
∴AO=8,BO=6,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}=\sqrt{{6}^{2}+{8}^{2}}$=10,
∴BC=CD=AD=AB=10,
∴菱形的周长为4×10=40,
故答案为:10;40
点评 本题考查了菱形对角线互相垂直平分的性质,考查了菱形各边长相等的性质,考查了勾股定理在直角三角形中的运用,根据勾股定理求AB的值是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
4.下列说法正确的是( )
| A. | 三角形的三个外角的和是180° | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 有两边和它们的夹角对应相等的两个三角形全等 | |
| D. | 如果两个三角形不全等,那么这两个三角形的面积一定不相等 |
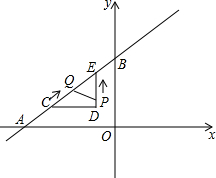 如图,直线y=$\frac{3}{4}$x+6交坐标轴于A、B两点,△CDE与△AOB形状完全相同,已知∠D=90°,CD=4,Q为△CDE斜边上的中点.点C从点A出发,以每秒5个单位长度的速度带动整个△CDE沿射线AB方向平移,同时,点P从顶点D出发,以每秒1个单位长度的速度沿直角边DE运动,当点P到达点E时,点P停止运动,△CDE也随之停止平移.设运动时间为t秒.
如图,直线y=$\frac{3}{4}$x+6交坐标轴于A、B两点,△CDE与△AOB形状完全相同,已知∠D=90°,CD=4,Q为△CDE斜边上的中点.点C从点A出发,以每秒5个单位长度的速度带动整个△CDE沿射线AB方向平移,同时,点P从顶点D出发,以每秒1个单位长度的速度沿直角边DE运动,当点P到达点E时,点P停止运动,△CDE也随之停止平移.设运动时间为t秒.