题目内容
如图，DE是△ABC中边AC的垂直平分线，若BC=18cm，AB=10cm，则△ABD的周长为（ ）| A、16cm | B、18cm |
| C、26cm | D、28cm |
考点：线段垂直平分线的性质
专题：
分析：根据线段的垂直平分线的性质定理可得AD=CD，据此即可求得△ABD的周长．
解答：解：∵DE是△ABC中边AC的垂直平分线，
∴AD=CD，
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=18+10=28（cm）．
故选D．
∴AD=CD，
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=18+10=28（cm）．
故选D．
点评：此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
相关题目
如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
实数a，b在数轴上对应的点如图所示，则下列式子中正确的是（ ）| A、-b+1＜0 |
| B、|a-1|=|b+1| |
| C、-b-a＞0 |
| D、2a+1＞0 |
已知k，n均为非负实数，且2k+n=2，则代数式2k2-4n的最小值为（ ）
| A、-40 | B、-16 | C、-8 | D、0 |
已知二次函数y=ax2+bx的图象如图所示，那么a、b的符号为（ ）| A、a＞0，b＞0； |
| B、a＜0，b＞0 |
| C、a＞0，b＜0 |
| D、a＜0，b＜0 |
代数式
的意义为（ ）
| x-y |
| 2 |
| A、x与y的一半的差 | ||
| B、x与y的差的一半 | ||
| C、x减去y除以2的差 | ||
D、x与y的
|
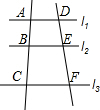如图，直线l1∥l2∥l3，已知：AB=4，BC=6，DE=3，则EF=（ ）| A、8 | B、6 | C、4.5 | D、2 |
一个多边形的每个内角都等于135°，则这个多边形的边数为（ ）
| A、7 | B、8 | C、9 | D、10 |