题目内容
16．已知x≥5的最小值为a，x≤-7的最大值为b，则ab=-35．分析 解答此题首先根据已知得出理解“≥”“≤”的意义，判断出a和b的最值即可解答．
解答 解：因为x≥5的最小值是a，a=5；
x≤-7的最大值是b，则b=-7；
则ab=5×（-7）=-35．
故答案为：-35．
点评 此题主要考查了不等式的解集的意义，解答此题要明确，x≥5时，x可以等于5；x≤5时，x可以等于5是解决问题的关键．
练习册系列答案
相关题目
6．
如图，将矩形纸片ABCD剪去一个角后，得到五边形ABCFE，则∠AEF+∠CFE的值为（ ）
如图，将矩形纸片ABCD剪去一个角后，得到五边形ABCFE，则∠AEF+∠CFE的值为（ ）| A． | 300° | B． | 270° | C． | 240° | D． | 180° |
7．
如图，边长为1的小正方形构成的网格中，⊙O半径为1，圆心O在格点上，则tan∠AED=（ ）
如图，边长为1的小正方形构成的网格中，⊙O半径为1，圆心O在格点上，则tan∠AED=（ ）| A． | 1 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
4．某商店举办促销活动，促销的方法是将原价x元的衣服以$\frac{3}{5}$（x-10）元出售，则下列说法中，能正确表达该商店促销方法的是（ ）
| A． | 原价减去10元后再打6折 | B． | 原价打6折后再减去10元 | ||
| C． | 原价减去10元后再打4折 | D． | 原价打4折后再减去10元 |
8．-$\frac{3}{4}$是下列各算式中（ ）的积．
| A． | -3$\frac{1}{2}$×（-$\frac{3}{14}$） | B． | $\frac{3}{4}$×（-$\frac{5}{6}$） | C． | （-1$\frac{1}{2}$）×$\frac{4}{9}$ | D． | $\frac{4}{5}$×（-$\frac{15}{16}$） |
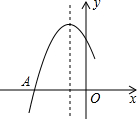如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1，下列结论：