题目内容
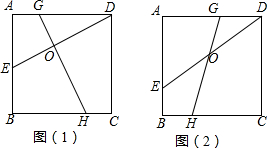
2. 如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20°,求∠OFE的度数.
分析 (1)由AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由已知角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由EF与OC平行,利用两直线平行同旁内角互补得到一对角互补,利用等角的补角相等得到∠BOC+∠DFE=180°,结合∠BOC+∠DFE=180°,求出∠OFE的度数即可.
解答 (1)证明:∵AB∥DC,
∴∠C=∠A,
∵∠1=∠A,
∴∠1=∠C,
∴FE∥OC;
(2)解:∵FE∥OC,
∴∠FOC+∠OFE=180°,
∵∠FOC+∠BOC=180°,∠DFE+∠OFE=180°,
∴∠BOC+∠DFE=180°,
∵∠BOC-∠DFE=20°,
∴∠BOC+∠DFE=180°,
解得:∠DFE=80°,
∴∠OFE=100°.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
13.下列命题是真命题的是( )
| A. | 内错角相等 | |
| B. | 如果a2=b2,那么a3=b3 | |
| C. | 三角形的一个外角大于任何一个内角 | |
| D. | 平行于同一直线的两条直线平行 |
7. 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )| A. | 60° | B. | 100° | C. | 110 | D. | 120° |
11.已知代数式$\frac{1}{2}$xa-1y3与-3xby2a-b是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
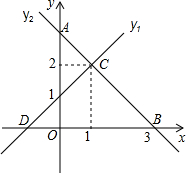 如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)
如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)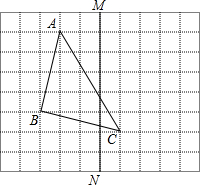 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.