题目内容
5.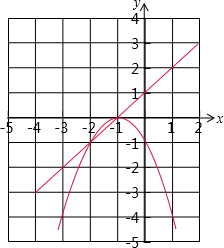 设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).
设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).(1)当k=1和k=2时的函数y1和y2的图象如图所示,请你在同一坐标系中画出k=3时函数y3的图象;
(2)根据图象,写出你发现的两条结论;
(3)将函数y3的图象向左平移2个单位,再向下平移4个单位,得到函数y4的图象.请写出函数y4的解析式,回答自变量x取何值时,函数y4的最小值是多少?
分析 (1)把k=3代入y=(x+1)[(k-2)x+(2k-3)]得到y=x2+4x+3,配方得到y=(x+2)2-1,所以函数y3的对称轴为直线x=-2,顶点坐标为(-2,-1),然后利用描点法画出函数y3的图象;
(2)利用函数图象经过固定点进行回答;
(3)利用点平移的规律得到点(-2,-1)平移所得对应点的坐标为(-4,-5),然后根据顶点式写出y4的解析式,然后根据二次函数的性质确定函数y4的最小值.
解答 解:(1)当k=3时,y3=(x+1)(x+3)=x2+4x+3=(x+2)2-1,
则函数y3的对称轴为直线x=-2,顶点坐标为(-2,-1),
如图,
(2)①图象都经过(-2,-1)和(-1,0);
②图象总交x轴于点(-1,0);
(3)函数y3的对称轴为直线x=-2,顶点坐标为(-2,-1),把点(-2,-1)向左平移2个单位,再向下平移4个单位所得对应点的坐标为(-4,-5),
所以函数y4的解析式为y=(x+4)2-5,
当x取-4时,函数y4的最小值是-5.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.也考查了二次函数的图象.

练习册系列答案
相关题目
17.小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:
假设月销售件数为x,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?
| 营业员 | 小张 | 小王 |
| 月销售件数 | 200 | 150 |
| 月总收入/元 | 1400 | 1250 |
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?
 如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE=4$\sqrt{3}$.
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE=4$\sqrt{3}$. 如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).
如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号). 如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.
如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$. 如图,AB=8,AD=AC=4,AE=2,∠BAD=∠CAE,AM⊥BC,AN⊥DE,则AM:AN=2.
如图,AB=8,AD=AC=4,AE=2,∠BAD=∠CAE,AM⊥BC,AN⊥DE,则AM:AN=2.