题目内容
2.直线OC、BC的函数关系式分别是y1=x和y2=2x+6,动点P(x,0)在OB上运动(0<x<3)过点P作直线m与x轴垂直.(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)设△COB中位于直线m左侧部分的面积为s,求出s与x之间函数关系式.
分析 (1)根据题意列出二元一次方程组,求出点C的坐标,结合图形求出y1>y2时x的取值范围;
(2)求出点B的坐标,根据三角形的面积公式解答.
解答 解:(1)由题意得,x=2x+6,
解得:x=-6,即可得点C的坐标为(-6,-6);
∵y1>y2,即x>2x+6,
解得:x<-6;
(2)y2=2x+6中当y=0时,x=-3,
则点B的坐标为(-3,0),
△COB中位于直线m左侧部分的面积为:s=$\frac{1}{2}$×3×(2x+6)=3x+9.
点评 本题考查的是一次函数与一元一次不等式的关系,掌握两条直线的交点的求法、灵活运用数形结合思想是解题的关键.

练习册系列答案
相关题目
12.一个长方体,无论从哪个角度看,不可能看到几个面( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.已知a+b=2,则a2-b2+4b的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
12.已知二次函数y=-$\frac{1}{2}$x2-3x-$\frac{5}{2}$,设自变量的值分别为x1,x2,x3,且-3<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y2>y3>y1 | D. | y2<y3<y1 |
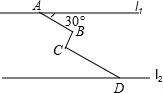 2016年清明小长假,所有高速公路对七座以下的机动车辆免收高速费,很多人都走出家门,投入大自然的环抱,进行自驾游.如图所示,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号)
2016年清明小长假,所有高速公路对七座以下的机动车辆免收高速费,很多人都走出家门,投入大自然的环抱,进行自驾游.如图所示,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号)
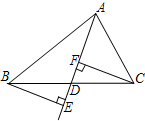 如图,已知BE⊥AD,CF⊥AD,BE=CF,由这三个条件组合运用可以得到若干结论,请你写出三个正确结论:△BDE≌△CDF,BD=CD,AD是△ABC的中线.
如图,已知BE⊥AD,CF⊥AD,BE=CF,由这三个条件组合运用可以得到若干结论,请你写出三个正确结论:△BDE≌△CDF,BD=CD,AD是△ABC的中线.